
21. (本小题满分12分)
已知函数
(Ⅰ)讨论 的单调性;
的单调性;
(Ⅱ)设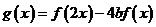 ,当
,当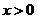 时,
时, ,求
,求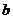 的最大值;
的最大值;
(Ⅲ)已知 ,估计
,估计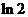 的近似值(精确到
的近似值(精确到 ).
).
请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题计分,做答时请写清题号.
(22)(本小题满分10分)选修4-1:几何证明选讲
 如图,
如图, 是
是 外一点,
外一点, 是切线,
是切线,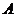 为切点,割线
为切点,割线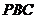 与
与 相交于点
相交于点 ,
, ,
, 为
为 的中点,
的中点, 的延长线交
的延长线交 于点
于点 ,证明:
,证明:
(I) ;
;
(II) .
.
(23)(本小题满分10分)选修4-4:坐标系与参数方程
在直角坐标系 中,以坐标原点为极点,
中,以坐标原点为极点,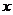 轴正半轴为极轴建立极坐标系,半圆
轴正半轴为极轴建立极坐标系,半圆 的极坐标方程为
的极坐标方程为
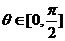 .
.
(I)求 的参数方程;
的参数方程;
(II)设点 在
在 上,
上, 在
在 处的切线与直线
处的切线与直线 垂直,根据(I)中你得到的参数方程,确定
垂直,根据(I)中你得到的参数方程,确定 的坐标.
的坐标.
(24)(本小题满分10分)选修4-5:不等式选讲
设函数
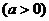 .
.
(I)证明: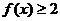 ;
;
(II)若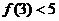 ,求
,求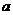 的取值范围.
的取值范围.
2014年普通高等学校招生全国统一考试
20. (本小题满分12分)
设 ,
, 分别是椭圆
分别是椭圆 的左、右焦点,
的左、右焦点, 是
是 上一点且
上一点且 与
与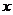 轴垂直,直线
轴垂直,直线 与
与 的另一个交点为
的另一个交点为 .
.
(Ⅰ)若直线 的斜率为
的斜率为 ,求
,求 的离心率;
的离心率;
(Ⅱ)若直线 在
在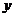 轴上的截距为
轴上的截距为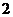 ,且
,且 ,求
,求 .
.
19. (本小题满分12分)
某地区2007年至2013年农村居民家庭人均纯收入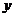 (单位:千元)的数据如下表:
(单位:千元)的数据如下表:
|
年份 |
2007 |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
年份代号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
人均纯收入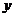 |
2.9 |
3.3 |
3.6 |
4.4 |
4.8 |
5.2 |
5.9 |
(Ⅰ)求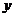 关于
关于 的线性回归方程;
的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
 ,
, .
.
18. (本小题满分12分)
 如图,四棱锥
如图,四棱锥 中,底面
中,底面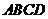 为矩形,
为矩形,
 平面
平面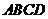 ,
, 为
为 的中点。
的中点。
(Ⅰ)证明: //平面
//平面 ;
;
(Ⅱ)设二面角 为
为 ,
, ,
,
 ,求三棱锥
,求三棱锥 的体积.
的体积.
三、解答题:解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)
已知数列 满足
满足 ,
, .
.
(Ⅰ)证明 是等比数列,并求
是等比数列,并求 的通项公式;
的通项公式;
(Ⅱ)证明: .
.
16.设点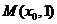 ,若在圆
,若在圆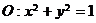 上存在点
上存在点 ,使得
,使得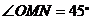 ,则
,则 的取值范围是________.
的取值范围是________.
15.已知偶函数 在
在 单调递减,
单调递减, .若
.若 ,则
,则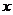 的取值范围是__ _.
的取值范围是__ _.
14.函数 的最大值为_________.
的最大值为_________.
二、填空题:本大题共4小题,每小题5分.
13. 的展开式中,
的展开式中,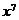 的系数为
的系数为 ,则
,则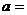 ________.(用数字填写答案)
________.(用数字填写答案)
12.设函数 .若存在
.若存在 的极值点
的极值点 满足
满足 ,则
,则 的取值范围是( )
的取值范围是( )
(A) (B)
(B) (C)
(C) (D)
(D)
第Ⅱ卷
本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生必须做答.第22题~第24题为选考题,考生根据要求做答.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com