
22、(本题满分14分)
已知椭圆 的方程为
的方程为 ,双曲线
,双曲线 的左、右焦点分别是
的左、右焦点分别是 的左、右顶点,而
的左、右顶点,而 的左、右顶点分别是
的左、右顶点分别是 的左、右焦点。
的左、右焦点。
(1)求双曲线 的方程;
的方程;
(2)若直线 与椭圆
与椭圆 及双曲线
及双曲线 都恒有两个不同的交点,且
都恒有两个不同的交点,且 与
与 的两个交点,A和B满足
的两个交点,A和B满足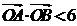 (其中O为原点),求
(其中O为原点),求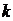 的范围。
的范围。
21、(本题满分14分)
已知数列 的前
的前 项和为
项和为 ,对一切正整数
,对一切正整数 ,点
,点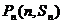 都在函数
都在函数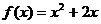 的图象上,且过点
的图象上,且过点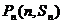 的切线的斜率为
的切线的斜率为 .
(1)求数列
.
(1)求数列 的通项公式;
(2)若
的通项公式;
(2)若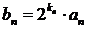 ,求数列
,求数列 的前
的前 项和
项和 ;
(3)设
;
(3)设 ,等差数列
,等差数列 的任一项
的任一项 ,其中
,其中 是
是 中的最小数,
中的最小数, ,求
,求 的通项公式.
的通项公式.
20、(本题满分12分)已知函数 ,其中
,其中 .
(1)讨论函数f(x)的单调性;
(2)当
.
(1)讨论函数f(x)的单调性;
(2)当 时,求函数f(x)的最大值.
时,求函数f(x)的最大值.
19、(本题满分12分)
如图,ABCD是边长为2的正方形 ,ED⊥平面ABCD,ED=1,EF∥BD且EF=
,ED⊥平面ABCD,ED=1,EF∥BD且EF=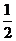 BD
BD (1)求证:BF∥平面ACE;
(1)求证:BF∥平面ACE;
(2)求二面角B-AF-C的大小;
(3)求点F到平面ACE的距离.
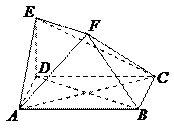
18、(本小题满分12分)
甲袋和乙袋中都装有大小相同的红球和白球,已知甲袋中共有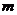 个球,乙袋中共有2
个球,乙袋中共有2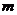 个球,从甲袋中摸出1个球为红球的概率为
个球,从甲袋中摸出1个球为红球的概率为 ,从乙袋中摸出1个球为红球的概率为
,从乙袋中摸出1个球为红球的概率为 .
.
(Ⅰ)若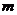 =10,求甲袋中红球的个数;
=10,求甲袋中红球的个数;
(Ⅱ)若将甲、乙两袋中的球装在一起后,从中摸出1个红 球的概率是
球的概率是 ,求
,求 的值;
的值;
(Ⅲ)设 =
= ,若从甲、乙两袋中各自有放回地摸球,每次摸出1个球,并且从甲袋中摸1次,从乙袋中摸2次. 设
,若从甲、乙两袋中各自有放回地摸球,每次摸出1个球,并且从甲袋中摸1次,从乙袋中摸2次. 设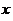 表示摸出红球的总次数,求
表示摸出红球的总次数,求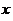 的分布列和数学期望.
的分布列和数学期望.
三、解答题:本大题共6小题,共76分。解答应写出文字说明,证明过程或演算步骤。
17、(本小题满分12分)
已知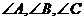 是三角形
是三角形 的三个内角,向量
的三个内角,向量
 ,且
,且
(I)求角A的大小;
(Ⅱ)若 ,求
,求 的值。
的值。
16、在实数的原有运算法则中,我们补充定义新运算“ ”如下:当
”如下:当 时,
时, ;当
;当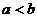 时,
时, .则函数
.则函数 的最大值是
的最大值是

15、 的值为
的值为
14、已知直线 与圆
与圆 交于A、B两个不同点,则实数
交于A、B两个不同点,则实数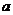 的取值范围为
的取值范围为
13、一个四面体共一个顶点的三条棱两两垂直,其长分别为 、
、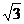 、2,且四面体的四个顶点在一个球面上,则这个球的体积为
、2,且四面体的四个顶点在一个球面上,则这个球的体积为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com