23、（本题10分） 为了测量学校旗杆AB的高度，学校数学实践小组做了如下实验：在阳光的照射下，旗杆AB的影子恰好落在水平地面BC的斜坡坡面CD上，测得BC=20m，CD=18m，太阳光线AD与水平面夹角为30°且与斜坡CD垂直．根据以上数据，请你求出旗杆AB的高度．（结果保留根号）

22、（本题10分）如图，一次函数y＝kx＋b(b<0)的图象与反比例函数y＝的图象交于点P，点P在第一象限，PA⊥x轴于点A，PB⊥y轴于点B．一次函数的图象分别交x轴、y轴于点C、D，且S△PAC＝1，，tan∠ACP＝．

(1)求点D的坐标；

(2)求一次函数与反比例函数的解析式：

(3)根据图象写出当x>0时，一次函数的值小于反比例函数

的值的x的取值范围．

21、(本题10分)某校组织340名师生外出活动，计划租用甲、乙两种型号的客车；经了解，甲车每辆最多能载40人和16件行李，乙车每辆最多能载30人和20件行李，

⑴已知师生行李打包后共有170件，若租用10辆甲、乙两种型号的客车，请你帮助设计出该校所有可行的租车方案，

⑵若师生行李打包后共有m件，且150＜m≤168，如果所租车辆刚好把所有师生和行李载走，(每辆车均以最多承载量载满)求m的值

20、(本题8分)我市的体育中考报考项目中，男生有三项内容：1000米跑(必考)；排球、篮球、足球(三选一)；实心球、立定跳远、1分钟跳绳(三选一)．除1000米跑外，小明的其余项目的平时测试成绩都是满分，所以，他决定随机选择．请用画树状图或列表的方法求：

⑴他选择的项目是1000米跑、排球、1分钟跳绳的概率是多少？

⑵他选择的项目中有立定跳远的概率是多少？(友情提醒：各个项目可用A、B、C、…等符号来代表可简化解答过程)

19、（本题8分）某学校为了了解学生的学习兴趣进行了一次抽样调查，学习兴趣情况分为三个层次，

A层次：很感兴趣，B层次：较感兴趣，C层次：不感兴趣. 将调查结果绘制成了

图①和图②的统计图（不完整）．请你根据图中提供的信息，解答下列问题：

（1）此次抽样调查中，共调查了200　　　 名学生；

（2）将图①补充完整；

（3）图②中C层次所在扇形的圆心角的度数是 　　　　度；

18、（本题8分）先化简，再求值：，其中满足x²-2x-4=0

三、解答题

17、（本题12分） （1）计算：

（2）解不等式组，并求出其最小整数解：

16、如图，已知直线y=－x+1分别交x轴、y轴于A、B两点，点M在x轴上，且满足

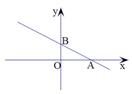∠OMB+∠BAO=45°,则点M的坐标为___________．

　　　 第15题　　　　　　　　 　　　　　　　第16题

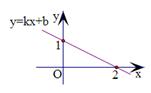
15、已知一次函数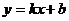的图象如图所示，则关于的不等式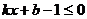的解集是_______．

14、正十二边形至少要绕它的中心旋转　　　 度，才能和原来的图形重合．