
17.(本小题满分1 5分)已知数列
5分)已知数列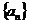 的前
的前 项和为
项和为 ,
,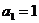 ,且
,且 (1)求数列
(1)求数列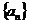 的通项公式;(2)对任意正整数
的通项公式;(2)对任意正整数 ,是否存在
,是否存在 ,使得
,使得 恒成立?若存在,求是实数
恒成立?若存在,求是实数 的最大值;若不存在,说明理由.
的最大值;若不存在,说明理由.
16.(本小题满分14分)在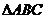 中,已知
中,已知 ,
, 且
且 .
.
(1)求角 和
和 的值;(2)若
的值;(2)若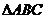 的边
的边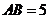 ,求边
,求边 的长.
的长.
二、解答题
15.(本小题满分14分)已知 .(1)当不等式
.(1)当不等式 的解集为
的解集为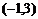 时, 求实数
时, 求实数 的值;(2)若对任意实数
的值;(2)若对任意实数
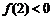
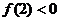 恒成立, 求实数
恒成立, 求实数 的取值范围. (3)设
的取值范围. (3)设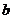 为常数,解关于
为常数,解关于 的不等式
的不等式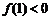 .
.

14.下面的数组均由三个数组成:(1,2,3),(2,4,6),(3,8,11),(4,16,20),
(5,32,37),…,(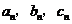 ).若数列{
).若数列{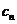 }的前
}的前 项和为
项和为 ,则
,则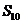 =
=
13.如果圆(x-2a)2+(y-a-3)2=4上总存在两个点到原点的距离为1,则实数a的取值范围是_____ ___.
12.在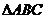 中,若
中,若 成等比数列,则
成等比数列,则 _________.
_________.
11.已知圆O: ,由直线
,由直线 上一点P作圆O的两条切线,切点为A,B,若在直线
上一点P作圆O的两条切线,切点为A,B,若在直线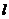 上至少存在一点P,使
上至少存在一点P,使 ,则k的取值范围是
.
,则k的取值范围是
.
10.已知首项为正数的等差数列 中,
中, .则当
.则当 取最大值时,数列
取最大值时,数列 的公差
的公差 .
.
9.已知钝角三角形ABC的最大边长是2,其余两边长分别是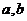 ,则集合
,则集合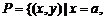
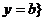 所表示的平面图形的面积是
;
所表示的平面图形的面积是
;
8.已知递增的等比数列 满足
满足 ,且
,且 的等差中项,
的等差中项,
若 ,则数列
,则数列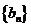 的前
的前 项和
项和 = .
= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com