
4.(3分)(2014•台湾)有一箱子装有3张分别标示4、5、6的号码牌,已知小武以每次取一张且取后不放回的方式,先后取出2张牌,组成一个二位数,取出第1张牌的号码为十位数,第2张牌的号码为个位数,若先后取出2张牌组成二位数的每一种结果发生的机会都相同,则组成的二位数为6的倍数的机率为何?( )
A. B. C. D.
分析:首先根据题意画出树状图,然后由树状图求得所有等可能的结果以及组成的二位数为6的倍数的情况,再利用概率公式即可求得答案.
解:画树状图得:
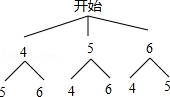
∵每次取一张且取后不放回共有6种可能情况,其中组成的二位数为6的倍数只有54,
∴组成的二位数为6的倍数的机率为.
故选A.
点评:本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
3.(3分)(2014•台湾)如图,梯形ABCD中,AD∥BC,E点在BC上,且AE⊥BC.若AB=10,BE=8,DE=6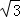 ,则AD的长度为何?( )
,则AD的长度为何?( )
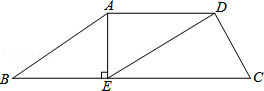
A.8 B.9 C.6 D.6
分析:利用勾股定理列式求出AE,再根据两直线平行,内错角相等可得∠DAE=90°,然后利用勾股定理列式计算即可得解.
解:∵AE⊥BC,
∴∠AEB=90°,
∵AB=10,BE=8,
∴AE===6,
∵AD∥BC,
∴∠DAE=∠AEB=90°,
∴AD== =6.
故选C.
点评:本题考查了梯形,勾股定理,是基础题,熟记定理并确定出所求的边所在的直角三角形是解题的关键.
2.(3分)(2014•台湾)若A为一数,且A=25×76×114,则下列选项中所表示的数,何者是A的因子?( )
A.24×5 B.77×113 C.24×74×114 D.26×76×116
分析:直接将原式提取因式进而得出A的因子.
解:∵A=25×76×114=24×74×114(2×72),
∴24×74×114,是原式的因子.
故选:C.
点评:此题主要考查了幂的乘方运算法则以及同底数幂的乘方,正确分解原式是解题关键.
一、选择题
1.(3分)(2014•台湾)算式(+×)×之值为何?( )
A.2 B.12 C.12 D.18
分析:先算乘法,再合并同类二次根式,最后算乘法即可.
解:原式=(+5)×
=6×
=18,
故选D.
点评:本题考查了二次根式的混合运算的应用,主要考查学生的计算能力,题目比较好,难度适中.
三、解答题:
19题 解:原式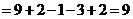
20题 解: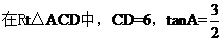
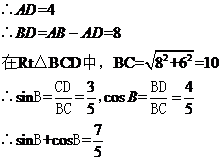
21题 解:原式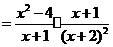
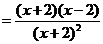

解方程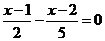 得:
得:
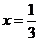
当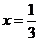 时,原式
时,原式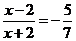
22题 解:(1) 22% ; 50 ;补充图形略
(2)由图可知:很不喜欢的共有3人,其中男性2人,女性1人.
画树状图如下:
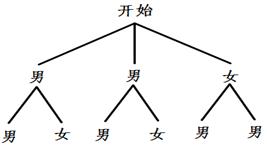
由图可知,共有6种等可能情况,其中恰好都是男性(记为事件A)有2种,其概率 .
.
23题 解:(1)设5月份在市区销售了x千克,则园区里销售了(3000-x)千克.
由题意得:
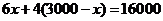
解得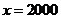 ,则
,则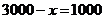
答:5月份在市区销售了2000千克,在园区销售了1000千克.
(2)由题意得:
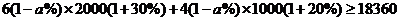
解得: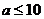
则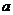 的最大值为10.
的最大值为10.
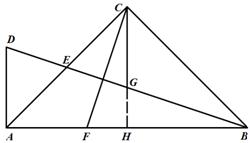 24题 证明:(1)∵∠ACB=90°,AC=BC,CG平分∠ACB
24题 证明:(1)∵∠ACB=90°,AC=BC,CG平分∠ACB
∴∠BCG=∠CAB=45°
又∵∠ACF=∠CBG,AC=BC
∴△ACF≌△CBG(ASA)
∴CF=BG,AF=CG.
(2)延长CG交AB于点H.
∵AC=BC,CG平分∠ACB
∴CH⊥AB,H为AB中点
又∵AD⊥AB
∴CH∥AD
∴G为BD的中点
∴BG=DG
∠D=∠EGC
∵E为AC中点
∴AE=EC
又∵∠AED=∠CEG
∴△AED≌△CEG(AAS)
∴DE=EG
∴BG=DG=2DE
由(1)得CF=BG
∴CF=2DE.
25题
解:(1)令x=0,解得y=3
 ∴点C的坐标为(0,3)
∴点C的坐标为(0,3)
令y=0,解得x1=-1,x2=3
∴点A的坐标为(-1,0)
点B的坐标为(3,0)
(2)由A,B两点坐标求得直线AB的解析式为y=-x+3
设点P的坐标为(x,-x+3)(0<x<3)
∵PM∥y轴
∠PNB=90°,点M的坐标为(x,-x2+2x+3)
∴PM=(-x2+2x+3)-(-x+3)
=-x2+3x
∵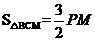
∴当x= 时
时 的面积最大
的面积最大
 此时,点P的坐标为(
此时,点P的坐标为( ,
,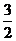 )
)
∴PN=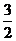 ,BN=
,BN=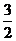 ,BP=
,BP=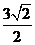
∴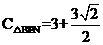 .
.
(3)求得抛物线对称轴为x=1
设点Q的坐标为(1, )
)
 ∴
∴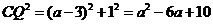
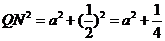
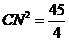
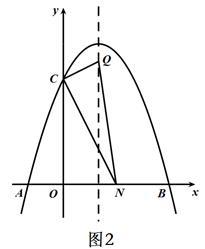
① 当∠CNQ=90°时, 如图1所示
即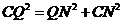
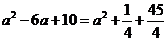
解得: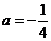
∴Q1(1,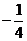 )
)
② 当∠NCQ=90°时,如图2所示
即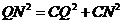
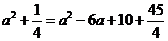
解得: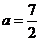
∴Q2(1,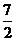 )
)
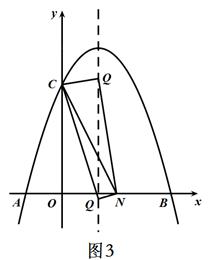
③ 当∠CQN=90°时,如图3所示
即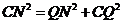
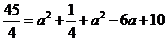
解得: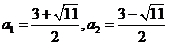
∴Q3(1,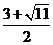 )Q4(1,
)Q4(1,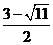 )
)
二、填空题:13、__12___ 14、_x≠2__ 15、__48___
16、__8 ___ 17、 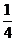 18、
18、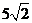
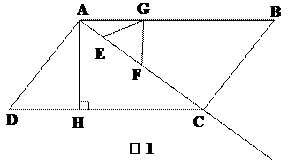
26、如图1,在□ABCD中,AH⊥DC,垂足为H,AB= ,AD=7,AH=
,AD=7,AH=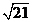 。现有两个动点E、F同时从点A出发,分别以每秒1个单位长度、每秒3个单位长度的速度沿射线AC方向匀速运动。在点E、F运动过程中,以EF为边作等边△EFG,使△EFG与△ABC在射线AC的同侧,当点E运动到点C时,E、F两点同时停止运动。设运转时间为t秒。
。现有两个动点E、F同时从点A出发,分别以每秒1个单位长度、每秒3个单位长度的速度沿射线AC方向匀速运动。在点E、F运动过程中,以EF为边作等边△EFG,使△EFG与△ABC在射线AC的同侧,当点E运动到点C时,E、F两点同时停止运动。设运转时间为t秒。
(1)求线段AC的长;
(2)在整个运动过程中,设等边△EFG与△ABC重叠部分的面积为S,请直接写出S与t之间的函数关系式,并写出相应的自变量t的取值范围;
(3)当等边△EFG的顶点E到达点C时,如图2,将△EFG绕着点C旋转一个角度
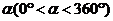 。在旋转过程中,点E与点C重合,F的对应点为F′,G的对应点为G′。设直线F′G′与射线DC、射线AC分别相交于M、N两点。试问:是否存在点M、N,使得△CMN是以∠MCN为底角的等腰三角形?若存在,请求出线段CM的长度;若不存在,请说明理由。
。在旋转过程中,点E与点C重合,F的对应点为F′,G的对应点为G′。设直线F′G′与射线DC、射线AC分别相交于M、N两点。试问:是否存在点M、N,使得△CMN是以∠MCN为底角的等腰三角形?若存在,请求出线段CM的长度;若不存在,请说明理由。


2014年重庆中考数学(B卷)答案
五、解答题:
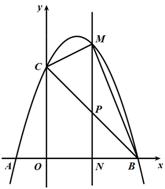
25、如图,已知抛物线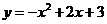 与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,连接BC。
与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,连接BC。
(1)求A、B、C三点的坐标;
(2)若点P为线段BC上的一点(不与B、C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当△BCM的面积最大时,求△BPN的周长;
 (3)在(2)的条件下,当BCM的面积最大时,在抛物线的对称轴上存在点Q,使得△CNQ为直角三角形,求点Q的坐标。
(3)在(2)的条件下,当BCM的面积最大时,在抛物线的对称轴上存在点Q,使得△CNQ为直角三角形,求点Q的坐标。
24、如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上一点,连接CF,且∠ACF=∠CBG。
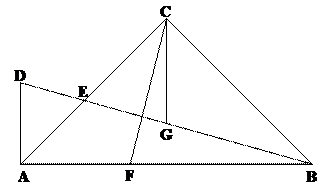 求证:(1)AF=CG;
求证:(1)AF=CG;
(2)CF=2DE
23、某生态农业园种植的青椒除了运往市区销售外,还可以让市民亲自去生态农业园购买。已知今年5月份该青椒在市区、园区的销售价格分别为6元/千克、4元/千克,今年5月份一共销售了3000千克,总销售额为16000元。
(1)今年5月份该青椒在市区、园区各销售了多少千克?
(2)6月份是青椒产出旺季,为了促销,生态农业园决定6月份将该青椒在市区、园区的销售价格均在今年5月份的基础上降低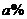 ,预计这种青椒在市区、园区的销量将在今年5月份的基础上分别增长30%、20%,要使得6月份该青椒的总销售额不低于18360元,则
,预计这种青椒在市区、园区的销量将在今年5月份的基础上分别增长30%、20%,要使得6月份该青椒的总销售额不低于18360元,则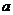 的最大值是多少?
的最大值是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com