14．(3分)(2014•台湾)小明在网络上搜寻到水资源的数据如下：「地球上水的总储量为1.36×10¹⁸立方公尺，其中可供人类使用的淡水只占全部的0.3%．」根据他搜寻到的数据，判断可供人类使用的淡水有多少立方公尺？(　)

A．4.08×10¹⁴　　　　　 B．4.08×10¹⁵　　　　　　 C．4.08×10¹⁶　　　　　　 D．4.08×10¹⁷

分析：科学记数法的表示形式为a×10ⁿ的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．

解：36×10¹⁸×0.3%＝4.08×10¹⁵．

故选：B．

点评：此题考查科学记数法的表示方法．科学记数法的表示形式为a×10ⁿ的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．

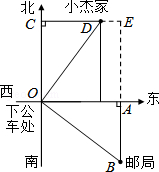
13．(3分)(2014•台湾)如图为小杰使用手机内的通讯软件跟小智对话的纪录．

根据图中两人的对话纪录，若下列有一种走法能从邮局出发走到小杰家，则此走法为何？(　)

A．向北直走700公尺，再向西直走100公尺

B．向北直走100公尺，再向东直走700公尺

C．向北直走300公尺，再向西直走400公尺

D．向北直走400公尺，再向东直走300公尺

分析：根据题意先画出图形，可得出AE＝400，AB＝CD＝300，再得出DE＝100，即可得出邮局出发走到小杰家的路径为：向北直走AB＋AE＝700公尺，再向西直走DE＝100公尺．

解：依题意，OA＝OC＝400＝AE，AB＝CD＝300，

DE＝400﹣300＝100，所以邮局出发走到小杰家的路径为，

向北直走AB＋AE＝700公尺，再向西直走DE＝100公尺．

故选A．

点评：本题考查了坐标确定位置，根据题意画出图形是解题的关键．

12．(3分)(2014•台湾)如图，D为△ABC内部一点，E、F两点分别在AB、BC上，且四边形DEBF为矩形，直线CD交AB于G点．若CF＝6，BF＝9，AG＝8，则△ADC的面积为何？(　)

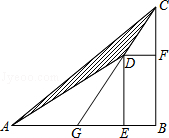
A．16　　　　　　　　　　 B．24　　　　　　　　　　　 C．36　　　　　　　　　　　 D．54

分析：由于△ADC＝△AGC﹣△ADG，根据矩形的性质和三角形的面积公式计算即可求解．

解：△ADC＝△AGC﹣△ADG

＝×AG×BC﹣×AG×BF

＝×8×(6＋9)﹣×8×9

＝60﹣36

＝24．

故选：B．

点评：考查了三角形的面积和矩形的性质，本题关键是活用三角形面积公式进行计算．

11．(3分)(2014•台湾)如图数轴上有A、B、C、D四点，根据图中各点的位置，判断那一点所表示的数与11﹣2最接近？(　)

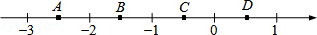
A．A　　　　　　　　　　　 B．B　　　　　　　　　　　　 C．C　　　　　　　　　　　　 D．D

分析：先确定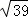的范围，再求出11﹣2的范围，根据数轴上点的位置得出即可．

解：∵6²＝36＜39＜42.25＝6.5²，

∴6＜＜6.5，

∴12＜2＜13，

∴﹣12＞﹣2＜﹣13，

∴﹣1＞11﹣2＜﹣2，

故选B．

点评：本题考查了数轴和估算无理数的大小的应用，解此题的关键是求出11﹣2的范围．

10．(3分)(2014•台湾)如图，有一圆通过△ABC的三个顶点，且的中垂线与相交于D点．若∠B＝74°，∠C＝46°，则的度数为何？(　)

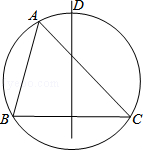
A．23　　　　　　　　　　 B．28　　　　　　　　　　　 C．30　　　　　　　　　　　 D．37

分析：由有一圆通过△ABC的三个顶点，且的中垂线与相交于D点．若∠B＝74°，∠C＝46°，可求得与的度数，继而求得答案．

解：∵有一圆通过△ABC的三个顶点，且的中垂线与相交于D点，

∴＝2×∠C＝2×46°═92°，＝2×∠B＝2×74°＝148°＝＋＝＋＝＋＋，

∴＝(148﹣92)＝28°．

故选B．

点评：此题考查了圆周角定理以及弧与圆心角的关系．此题难度不大，注意掌握数形结合思想的应用．

9．(3分)(2014•台湾)如图，坐标平面上，△ABC与△DEF全等，其中A、B、C的对应顶点分别为D、E、F，且AB＝BC＝5．若A点的坐标为(﹣3，1)，B、C两点在方程式y＝﹣3的图形上，D、E两点在y轴上，则F点到y轴的距离为何？(　)

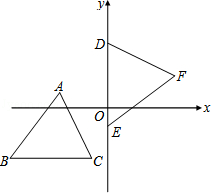
A．2　　　　　　　　　　　 B．3　　　　　　　　　　　　 C．4　　　　　　　　　　　　 D．5

分析：如图，作AH、CK、FP分别垂直BC、AB、DE于H、K、P．由AB＝BC，△ABC≌△DEF，就可以得出△AKC≌△CHA≌△DPF，就可以得出结论．

解：如图，作AH、CK、FP分别垂直BC、AB、DE于H、K、P．

∴∠DPF＝∠AKC＝∠CHA＝90°．

∵AB＝BC，

∴∠BAC＝∠BCA．

在△AKC和△CHA中。

∴△AKC≌△CHA(ASA)，

∴KC＝HA．

∵B、C两点在方程式y＝﹣3的图形上，且A点的坐标为(﹣3，1)，

∴AH＝4．

∴KC＝4．

∵△ABC≌△DEF，

∴∠BAC＝∠EDF，AC＝DF．

在△AKC和△DPF中，

∴△AKC≌△DPF(AAS)，

∴KC＝PF＝4．

故选C．

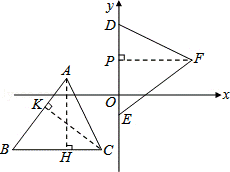
点评：本题考查了坐标与图象的性质的运用，垂直的性质的运用，全等三角形的判定及性质的运用，等腰三角形的性质的运用，解答时证明三角形全等是关键．

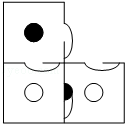
8．(3分)(2014•台湾)下列选项中有一张纸片会与如图紧密拼凑成正方形纸片，且正方形上的黑色区域会形成一个轴对称图形，则此纸片为何？(　)

A．　　　　 B．　　　　　 C．　　　　　 D．

分析：根据轴对称图形的概念：如果一个图形沿着一条直线对折，直线两侧的图形能够完全重合，这个图形就是轴对称图形可得答案．

解：如图所示：

故选：A．

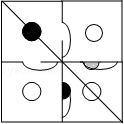
点评：此题主要考查了利用轴对称设计图案，关键是掌握轴对称图形的概念．

7．(3分)(2014•台湾)已知果农贩卖的西红柿，其重量与价钱成线型函数关系，今小华向果农买一竹篮的西红柿，含竹篮秤得总重量为15公斤，付西红柿的钱250元．若他再加买0.5公斤的西红柿，需多付10元，则空竹篮的重量为多少公斤？(　)

A．1.5　　　　　　　　　　 B．2　　　　　　　　　　　　 C．2.5　　　　　　　　　　 D．3

分析：由加买0.5公斤的西红柿，需多付10元就可以求出西红柿的单价，再由总价250元÷西红柿的单价就可以求出西红柿的数量，进而求出结论．

解：由题意，得

西红柿的单价为：10÷0.5＝20元，

西红柿的重量为：250÷20＝12.5kg，

∴空竹篮的重量为：15﹣12.5＝2.5kg．

故选C．

点评：本题考查了总价÷数量＝单价的运用，总价÷单价＝数量的运用，解答时求出西红柿的单价是解答本题的关键．

6．(3分)(2014•台湾)若二元一次联立方程式的解为x＝a，y＝b，则a＋b之值为何？(　)

A．　　　　　　　　　　　 B．　　　　　　　　　　　 C．　　　　　　　　　　　 D．

分析：首先解方程组求得x、y的值，即可得到a、b的值，进而求得a＋b的值．

解：解方程组得：

则a＝，b＝，

则a＋b＝＝．

故选A．

点评：此题主要考查了二元一次方程组解法，解方程组的基本思想是消元，正确解方程组是关键．

5．(3分)(2014•台湾)算式743×369﹣741×370之值为何？(　)

A．﹣3　　　　　　　　　 B．﹣2　　　　　　　　　　 C．2　　　　　　　　　　　　 D．3

分析：根据乘法分配律，可简便运算，根据有理数的减法，可得答案．

解：原式＝743×(370﹣1)﹣741×370

＝370×(743﹣741)﹣743

＝370×2﹣743＝﹣3，

故选：A．

点评：本题考查了有理数的乘法，乘法分配律是解题关键．