
5.下列性质中,正方形具有而矩形不一定具有的性质是
 A.4个角都是直角 B.对角线互相垂直 C.对角线相等 D.对角线互相平分
A.4个角都是直角 B.对角线互相垂直 C.对角线相等 D.对角线互相平分
4.估算
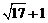 的值
的值 在
在
A.2和3之间 B.3和4之间 C.4和5之间 D.5和6之间
3.方程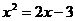 的根的情况是
的根的情况是
A.有一个实数根 B.有两个相等的实数根
C.有两个不相等的实数根 D.没有实数根
2.关于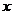 的一元二次方程
的一元二次方程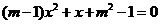 的一个根是0,则
的一个根是0,则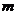 的值为
的值为
A.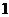
 B.
B.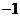 C.
C.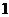 或
或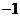
 D.0.5
D.0.5
一、选择题
1.下列 各式中,与
各式中,与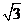 是同类二次根式的是
是同类二次根式的是
A. B.
B.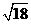 C.
C.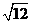 D.
D.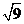
29.(2014•台湾)如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE.请完整说明为何△ABC与△DEC全等的理由.
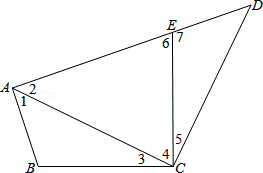
分析:根据∠BCE=∠ACD=90°,可得∠3=∠5,又根据∠BAE=∠1+∠2=90°,∠2+∠D=90°,可得∠1=∠D,继而根据AAS可判定△ABC≌△DEC.
解:∵∠BCE=∠ACD=90°,
∴∠3+∠4=∠4+∠5,
∴∠3=∠5,
在△ACD中,∠ACD=90°,
∴∠2+∠D=90°,
∵∠BAE=∠1+∠2=90°,
∴∠1=∠D,
在△ABC和△DEC中,
∴△ABC≌△DEC(AAS).
点评:本题考查了全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
二、非选择题
28.(2014•台湾)已知甲校有a人,其中男生占60%;乙校有b人,其中男生占50%.今将甲、乙两校合并后,小清认为:「因为=55%,所以合并后的男生占总人数的55%.」如果是你,你会怎么列式求出合并后男生在总人数中占的百分比?你认为小清的答案在任何情况都对吗?请指出你认为小清的答案会对的情况.请依据你的列式检验你指出的情况下小清的答案会对的理由.
分析:根据加权平均数的计算公式可得合并后男生在总人数中占的百分比,再与小清的结果进行比较即可.
解:合并后男生在总人数中占的百分比是:×100%.
当a=b时小清的答案才成立;
当a=b时,×100%=55%.
点评:此题考查了加权平均数,关键是根据加权平均数的计算公式列出算式,再进行比较.
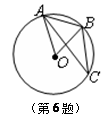
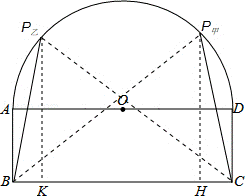
27.(3分)(2014•台湾)如图,矩形ABCD中,AD=3AB,O为AD中点,是半圆.甲、乙两人想在上取一点P,使得△PBC的面积等于矩形ABCD的面积其作法如下:
(甲) 延长BO交于P点,则P即为所求;
(乙) 以A为圆心,AB长为半径画弧,交于P点,则P即为所求.
对于甲、乙两人的作法,下列判断何者正确?( )

A.两人皆正确 B.两人皆错误 C.甲正确,乙错误 D.甲错误,乙正确
分析:利用三角形的面积公式进而得出需P甲H=P乙K=2AB,即可得出答案.
解:要使得△PBC的面积等于矩形ABCD的面积,
需P甲H=P乙K=2AB.
故两人皆错误.
故选:B.
点评:此题主要考查了三角形面积求法以及矩形的性质,利用四边形与三角形面积关系得出是解题关键.
26.(3分)(2014•台湾)已知a、h、k为三数,且二次函数y=a(x﹣h)2+k在坐标平面上的图形通过(0,5)、(10,8)两点.若a<0,0<h<10,则h之值可能为下列何者?( )
A.1 B.3 C.5 D.7
分析:先画出抛物线的大致图象,根据顶点式得到抛物线的对称轴为直线x=h,由于抛物线过(0,5)、(10,8)两点.若a<0,0<h<10,则点(0,5)到对称轴的距离大于点(10,8)到对称轴的距离,所以h﹣0>10﹣h,然后解不等式后进行判断.
解:∵抛物线的对称轴为直线x=h,
而(0,5)、(10,8)两点在抛物线上,
∴h﹣0>10﹣h,解得h>5.
故选D.

点评:本题考查了二次函数图象与系数的关系:二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小,当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置,当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点.抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定,△=b2﹣4ac>0时,抛物线与x轴有2个交点;△=b2﹣4ac=0时,抛物线与x轴有1个交点;△=b2﹣4ac<0时,抛物线与x轴没有交点.
25.(3分)(2014•台湾)有甲、乙两个箱子,其中甲箱内有98颗球,分别标记号码1~98,且号码为不重复的整数,乙箱内没有球.已知小育从甲箱内拿出49颗球放入乙箱后,乙箱内球的号码的中位数为40.若此时甲箱内有a颗球的号码小于40,有b颗球的号码大于40,则关于a、b之值,下列何者正确?( )
A.a=16 B.a=24 C.b=24 D.b=34
分析:先求出甲箱的球数,再根据乙箱中位数40,得出乙箱中小于、大于40的球数,从而得出甲箱中小于40的球数和大于40的球数,即可求出答案.
解:甲箱98﹣49=49(颗),
∵乙箱中位数40,
∴小于、大于40各有(49﹣1)÷2=24(颗),
∴甲箱中小于40的球有39﹣24=15(颗),大于40的有49﹣15=34(颗),即a=15,b=34.
故选D.
点评:此题考查了中位数,掌握中位数的定义是本题的关键,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com