
一、选择题
1.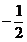 的相反数是
( ▲
的相反数是
( ▲  )
)
A.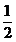 B.
B.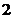 C.
C.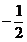 D.
D.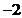
三、解答题17、18题各8分
17解: 18.解:

 19.(8分)题设:
;结论:
.(均填写序号)
19.(8分)题设:
;结论:
.(均填写序号)
证明:

 20.(满分8分)
20.(满分8分)
解:(1)
(2)点A的坐标是( , ),
点 的坐标是( , );
的坐标是( , );
(3)点P的坐标是( , ).
 21.(满分8分)
21.(满分8分)
解:(1)此次抽样调查中,共调查了 个学生家长;
(2)将图1,图2补充完整;
(3)根据调查结果,请你估计该校这1800个学生家长中,持反对态度的有 人.


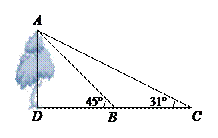 22.(满分10分)
22.(满分10分)
解:
 23.(满分10分)
23.(满分10分)
解:

24.(满分12分)
解:(1)填空:抛物线的顶点坐标是( , ),对称轴是 ;
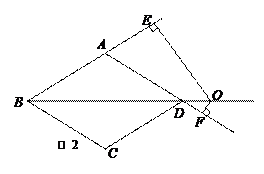
 25.(满分14分)
25.(满分14分)
解:(1)抛物线y=x2-1 直角抛物线;


(备用图)
15. 16.
二、填空题
11. 12. 13. 14.
25.(满分14分)定义:若抛物线y=ax2+bx+c与x轴的两个交点和顶点构成直角三角形,则称这条抛物线为“直角抛物线”.
(1)抛物线y=x2-1 直角抛物线(填“是”或“不是”);
(2)如图,直角抛物线y=x2+4x+c与x轴交于点A、B(A在B的左侧),与y轴交于点C,顶点为P.
① 求c的值;
② 在x轴上是否存在点Q,使得以A、Q、C为顶点的三角形与△APB相似?若存在,
求出点Q的坐标;若不存在,请说明理由;
(3)观察(1)、(2)中的抛物线解析式,试猜想:在直角抛物线y=ax2+bx+c(a>0)中,b2-4ac是否为定值?若是,请直接写出该定值.(不要求说理)


(第25题) (备用图)
2014年漳州市初中毕业班质量检测考试--数学答题卡


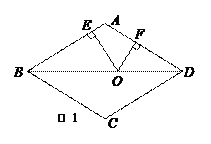
24.(满分12分)如图,在边长为10的菱形ABCD中,对角线BD=16,点O是直线BD上的动点,OE⊥AB于E,OF⊥AD于F.
(1)对角线AC的长是 ,菱形ABCD的面积是 ;
(2)如图1,当点O在对角线BD上运动时,OE+OF的值是否发生变化?请说明理由;
(3)如图2,当点O在对角线BD的延长线上时,OE+OF的值是否发生变化?
 若不变请说明理由,若变化,请探究OE、OF之间的数量关系,并说明理由.
若不变请说明理由,若变化,请探究OE、OF之间的数量关系,并说明理由.
(第24题)
23.(满分10分)某校奖励在《中国梦·我的梦》演讲比赛中获奖的同学,派陈老师去购买奖品.陈老师决定在标价为8元/本笔记本和标价为25元/支的钢笔中选购,设购买钢笔x(x>0)支.
(1)售货员说:“若购买钢笔超过10支,则超出部分可以享受8折优惠,而购买笔记本不优惠.”设购买钢笔需要y元,请你求出y与x的函数关系式;
(2)陈老师根据学校设奖要求,决定购买笔记本和钢笔总数为30,且笔记本数不多于钢笔数的一半.设总费用为w元,请问如何购买总费用最少?
22.(满分10分)南靖云水谣古村落中有一棵高大的老榕树.小明为测量该榕树的高度AD,在大树前的平地上点C处测得大树顶端A的仰角∠C=31°,然后向前直走23米到达B处,又测得大树顶端A的仰角∠ABD=45°,已知C、B、D在同一直线上(如图所示),
求老榕树的高度AD.(参考数据:tan31°≈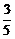 ,sin31°≈
,sin31°≈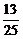 )
)
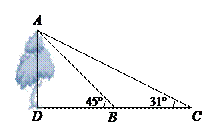

(第22题)
18.(满分8分)解方程组: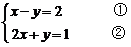
 19.(满分8分)如图,在△ABC和△ADE中,B、D、C三点在同一直线上.有以下四个条件:① AB=AD,② ∠B=∠ADE,③ ∠1=∠2,④ BC=DE.
19.(满分8分)如图,在△ABC和△ADE中,B、D、C三点在同一直线上.有以下四个条件:① AB=AD,② ∠B=∠ADE,③ ∠1=∠2,④ BC=DE.
请你从这四个条件中选出三个作为题设,另一个作为结论,组成
一个真命题(均用序号表示),并给予证明.
(第19题)
 20.(满分8分)如图,把直角坐标系xoy放置在边长为1的
20.(满分8分)如图,把直角坐标系xoy放置在边长为1的
正方形网格中,O是坐标原点,点A、O、B均在格点上,
将△OAB绕O点按顺时针方向旋转90°后,得到△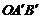 .
.
(1)画出△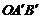 ;
;
(2)点A的坐标是( , ),
点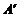 的坐标是( , );
的坐标是( , );
(3)若点P在y轴上,且PA+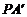 的值最小,
的值最小,
则点P的坐标是( , ). (第20题)
 21.(满分8分)中学生骑电动车上学给交通带来隐患.某中学在该校1800个学生家长中,随机调查了部分家长对“中学生骑电动车上学”的态度(态度分为:A.反对,B.无所谓,C.赞成),并将调查结果绘制成图1和图2的统计图(不完整).请根据图中提供的信息,解答下列问题:
21.(满分8分)中学生骑电动车上学给交通带来隐患.某中学在该校1800个学生家长中,随机调查了部分家长对“中学生骑电动车上学”的态度(态度分为:A.反对,B.无所谓,C.赞成),并将调查结果绘制成图1和图2的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 个学生家长;
(2)将图1,图2补充完整;
(3)根据调查结果,请你估计该校这1800个学生家长中,持反对态度的有 人.
三、解答题
17.(满分8分)先化简,再求值:(a-1)2-a(a+1),其中a=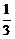
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com