
5. 已知函数f(x)=sin(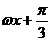 )(
)(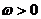 )的最小正周期为
)的最小正周期为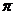 ,则该函数的图象
,则该函数的图象
关于( )对称
A.点(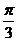 ,0)
B.直线x=
,0)
B.直线x=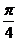 C.点(
C.点(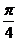 ,0) D.直线x=
,0) D.直线x=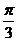
4. 已知向量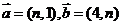 ,则
,则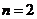 是
是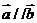 ( )条件,
( )条件,
A.充分不必要 B.必要不充分 C.充要 D.既不充分又不要必
3. 设等差数列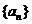 的前
的前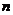 项和为
项和为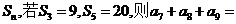 ( )
( )
A.63 B.45 C.36 D.27
2. 已知i为虚数单位, 则复数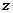
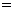 i
i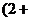 i
i 在复平面内对应的点位于( )
在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
一、选择题
1. 设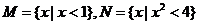 ,则
,则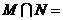 (
)
(
)
A.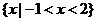 B.
B.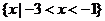 C.
C.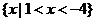 D.
D.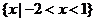
28.(本题满分12分)如图,经过原点的抛物线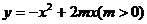 与
与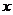 轴的另一个交点为A.过点P(1,
轴的另一个交点为A.过点P(1,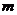 )作直线PM⊥
)作直线PM⊥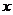 轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(B、C不重合).连结CB,CP.
轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(B、C不重合).连结CB,CP.
(1)当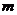 =3时,求点A的坐标和BC的长;
=3时,求点A的坐标和BC的长;
(2)当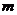 >1时,连结CA,当CA⊥CP时,求
>1时,连结CA,当CA⊥CP时,求 的值.
的值.
(3)过点P作PE⊥PC且PE=PC,问是否存在 ,使得点E落在坐标轴上?若存在,求出所有满足要求的
,使得点E落在坐标轴上?若存在,求出所有满足要求的 的值,并写出相对应的点E坐标;若不存在
的值,并写出相对应的点E坐标;若不存在 ,请说明理由.
,请说明理由.
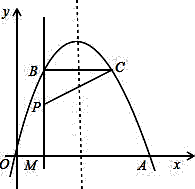
27.(本题满分12分)如图1,在Rt△ABC中,∠ACB=90°,∠A=30°,P为BC边上任意一点,点Q为AC边上的动点,分别以CP、PQ为边作等边△PCF和等边△PQE,连接EF.
(1)直接写出图1中EF与AB的位置关系: ▲ ;
(2)如图2,当点P为BC延长线上任意一点时,(1)中的结论是否成立?请说明理由.
(3)如图3,在Rt△ABC中,∠ACB=90°,∠A=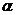 °,P为BC延长线上一点,点Q为AC边上的动点,分别以CP、PQ为腰作等腰△PCF和等腰△PQE,使得PC=PF,PQ=PE,连接EF.当△PCF和△PQE满足什么条件时,(1)中的结论仍然成立?为什么?
°,P为BC延长线上一点,点Q为AC边上的动点,分别以CP、PQ为腰作等腰△PCF和等腰△PQE,使得PC=PF,PQ=PE,连接EF.当△PCF和△PQE满足什么条件时,(1)中的结论仍然成立?为什么?


25.(本题满分10分)如图,AB为⊙O的直径,点C在⊙O 上,点P是直径AB上的一点,(不与A、B重合),过点P作AB的垂线交BC的延长线于点Q.
 (1)点D在线段PQ上,且DQ=DC
(1)点D在线段PQ上,且DQ=DC . 求证:CD是⊙O的切线;
. 求证:CD是⊙O的切线;
(2)若cosB=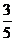 ,BP =6,AP =
,BP =6,AP = ,求QC的长.
,求QC的长.
如图1,在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,过A作 AD⊥BC于D,则sinB=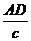 ,sinC=
,sinC=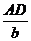 ,即AD=csinB,AD=bsinC,于是csinB=bsinC,即
,即AD=csinB,AD=bsinC,于是csinB=bsinC,即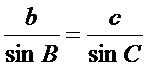 .同理有:
.同理有: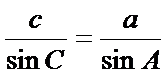 ,
,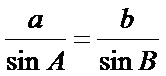 ,所以
,所以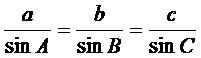 .即:在一个三角形中,各边和它所对角的正弦的比相等.在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论就可以求出其余三个未知元素.
.即:在一个三角形中,各边和它所对角的正弦的比相等.在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论就可以求出其余三个未知元素.
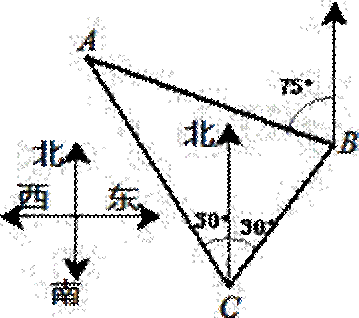
(1)如图2,一货轮在C处测得灯塔A在货轮的北偏西30°的方向上,随后货轮以60海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得灯塔 A在货轮的北偏西75°的方向上,求此时货轮距灯塔A的距离AB.
A在货轮的北偏西75°的方向上,求此时货轮距灯塔A的距离AB.
(2)在(1)的条件下,试求75°的正弦值.(结果保留根号)

|
|
24.(本题满分10分)某校为了进一步开展“阳光体育”活动,计划用2000元购买乒乓球拍,用2800元购买羽毛球拍,已知一副羽毛球拍比一副乒乓球拍贵14元.该校购买的乒 乓球拍与羽毛球拍的数量能相同吗?
乓球拍与羽毛球拍的数量能相同吗?
(1)根据题意,甲、乙两位同学都先假设该校购买的乒乓球拍与羽毛球拍的数量能相同,并分别列出的方程如下:
甲: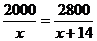 ; 乙:
; 乙: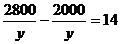 .
.
根据两位同学所列的方程,请你分别指出未知数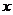 ,
,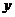 表示的意义:
表示的意义:
甲: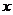 表示
▲ ;
表示
▲ ;
乙: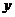 表示
▲
表示
▲
 ;
;
(2)该校购买的乒乓球拍与羽毛球拍的数量能相同吗?请说明理由.(写出完整的解答过程)
23.(本题满分10分)田忌赛马的故事为我们所熟知.小亮与小齐学习概率初步知识后设计了如下游戏:小亮手中有方块l0、8、6三张扑克牌,小齐手中有方块9、7、5三张扑克牌.每人从各自手中取一张牌进行比较,数字大的为本“局”获胜,每次取的牌不能放回.
(1)若每人随机取手中的一张牌进行比赛,通过列表格或画树状图求小齐本“局”获胜的概率;
(2)若比赛采用三局两胜制,即胜2局或3局者为本次比赛获胜者.当小亮的三张牌出牌顺序为先出6,再出8,最后出l0时,小齐随机出牌应对,求小齐本次比 赛获胜的概率.
赛获胜的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com