
5、下列判断错误的是( )
A.若a=b,则a-3=b-3
B.若a=b,则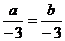
C. 若ax=bx,则a=b D. 若x=2,则x2=2x
4、下列计算正确的是( )
A.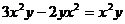 B.
B.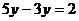
C.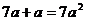 D.
D.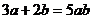
3、 在下列各数
在下列各数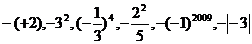 中,负数的个数是( )
中,负数的个数是( )
A.2 B.3 C.4 D.5
2、温家宝总理有句名言:多么小的问题乘以13亿,都会变得很大;多么大的经济总量,除以13亿都会变得很小.将1 300 000 000用科学记数法表示为( )
A.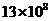 B.
B.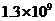 C.
C.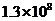 D.
D.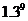
一、 你一定能选对!
1、5的相反数是( )
A.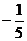 B.
B.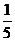 C.
C.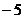 D.5
D.5
20.(本小题满分16分)
已知数列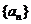 满足:
满足: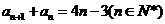
(1)若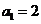 ,求数列
,求数列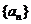 的前20项和
的前20项和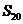 ;
;
(2)若对于任意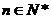 ,都有
,都有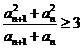 成立,求
成立,求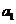 的取值范围;
的取值范围;
(3)若数列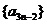 (
(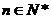 )为等差数列,求证:数列
)为等差数列,求证:数列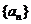 为等差数列.
为等差数列.
解:(1)因为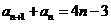 ,
,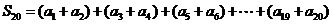
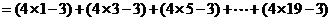
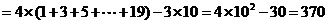 …………4分
…………4分
(2)因为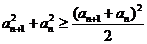 ……………5分
……………5分
又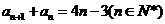 ,所以
,所以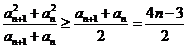
要使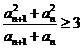 对于任意
对于任意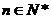 恒成立,只要
恒成立,只要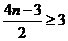 成立,即
成立,即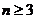
所以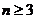 ,
,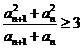 恒成立…………7分
恒成立…………7分
为保证任意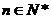 恒成立,所以只要
恒成立,所以只要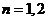 ,
,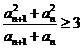 成立即可,即
成立即可,即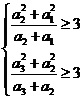
当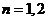 时,
时,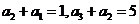 ,所以
,所以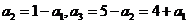 ,
,
所以只要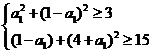 ,解得
,解得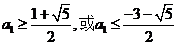 ………9分
………9分
(3)因为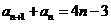 ,
,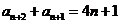 ,所以
,所以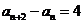 ,
,
所以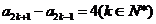 ,
,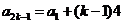 ①……………10分
①……………10分
又因为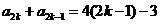 ,
,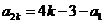 ②……………11分
②……………11分
因为数列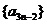 (
(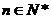 )为等差数列,所以
)为等差数列,所以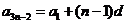 ③……………12分
③……………12分
在③中分别取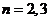 得到
得到 ④,
④,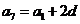 ⑤,
⑤,
在②中取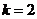 得
得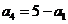 ⑥,在①中取
⑥,在①中取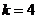 ,
,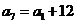 ⑦
⑦
由④⑤⑥⑦得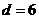 ,
,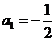 …………14分
…………14分
代入① ②分别得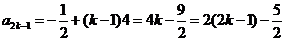 ,
,
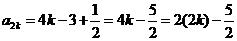 ,
,
当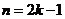 时,
时, ;当
;当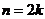 时,
时, ,
,
综上所述 ,
,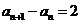 ,所以数列
,所以数列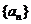 为等差数列……16分
为等差数列……16分
19.(本小题满分16分)
已知函数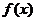 是区间
是区间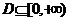 上的增函数,若
上的增函数,若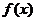 可表示为
可表示为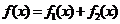 ,
,
其中 是区间
是区间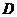 上的增函数,
上的增函数,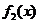 是区间
是区间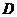 上的减函数,且函数
上的减函数,且函数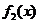 的值域
的值域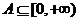 ,则称函数
,则称函数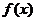 是区间
是区间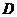 上的“偏增函数”.
上的“偏增函数”.
(1)试说明函数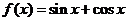 是区间
是区间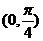 上的“偏增函数”;
上的“偏增函数”;
(2)记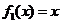 ,
,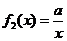 (
( 为常数),试判断函数
为常数),试判断函数 是区间
是区间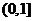 上的“偏增函数”,若是,证明你的结论;若不是,请说明理由
上的“偏增函数”,若是,证明你的结论;若不是,请说明理由
解:(1)因为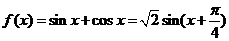 是区间
是区间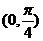 上增函数,………3分
上增函数,………3分
记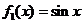 ,
,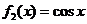 ,显然
,显然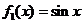 是区间
是区间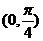 上增函数
上增函数
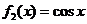 是区间
是区间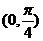 上减函数,且
上减函数,且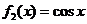 的值域
的值域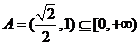
………5分
(2)函数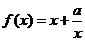 不是区间
不是区间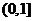 上的“偏增函数”………7分
上的“偏增函数”………7分
理由如下:显然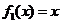 是区间
是区间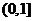 上的增函数,
上的增函数,
当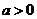 时,
时,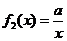 是区间
是区间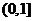 上的减函数,
上的减函数,
要使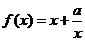 是区间
是区间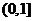 上的“偏增函数”,只要
上的“偏增函数”,只要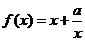 是区间
是区间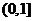 上的增函数,………10分
上的增函数,………10分
当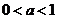 时,易用定义证明
时,易用定义证明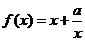 在
在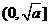 上是减函数,
上是减函数,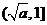 上是增函数,
上是增函数,
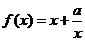 不是区间
不是区间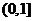 上的增函数,………12分,
上的增函数,………12分,
当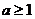 时,易用定义证明
时,易用定义证明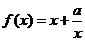 在
在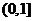 上是减函数,
上是减函数,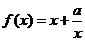 不是区间
不是区间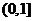 上的增函数,………14分
上的增函数,………14分
综上所述,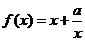 不是区间
不是区间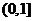 上的增函数,
上的增函数,
所以函数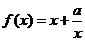 也不是区间
也不是区间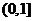 上的“偏增函数”,………16分
上的“偏增函数”,………16分
18.(本小题满分16分)
某水库堤坝因年久失修,发生了渗水现象,经测算坝面每渗水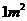 的直接经济损失约为250元。当发现时已有
的直接经济损失约为250元。当发现时已有 的坝面渗水.且渗水还在以每天
的坝面渗水.且渗水还在以每天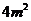 的速度扩散. 当地政府在发现的同时立即组织民工抢修,假定每位民工平均每天可抢修渗水面积
的速度扩散. 当地政府在发现的同时立即组织民工抢修,假定每位民工平均每天可抢修渗水面积 ,为此政府需支出服装补贴费每人400元,劳务费每人每天150元,所消耗的维修材料等费用每人每天150元.若安排
,为此政府需支出服装补贴费每人400元,劳务费每人每天150元,所消耗的维修材料等费用每人每天150元.若安排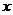 名民工参与抢修,抢修完成需用
名民工参与抢修,抢修完成需用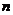 天。
天。
(1)写出n关于x的函数关系式;
(2)应安排多少名民工参与抢修,才能使总损失最小, (总损失=渗水损失+政府支出).
解:(1)由题意得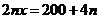 ,所以
,所以 ,
,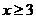 ,
, ………4分
………4分
(2)设总损失为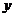 ,则
,则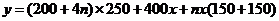 ……8分
……8分
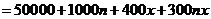
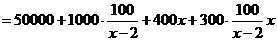
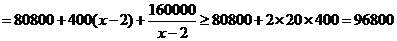 ………14分
………14分
当且仅当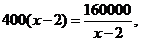 即
即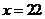 时,等号成立………15分
时,等号成立………15分
答:应安排22名民工参与抢修,才能使总损失最小………16分
17.(本小题满分14分)
已知二次函数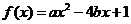
(1)设集合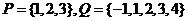 ,分别从集合
,分别从集合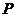 和
和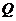 中随机取一个数作为
中随机取一个数作为 和
和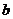 ,求函数
,求函数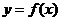 在区间
在区间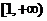 上是增函数的概率;
上是增函数的概率;
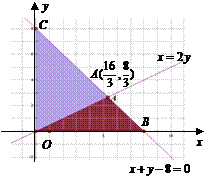
(2)设点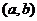 是区域
是区域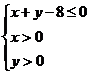 内的随机点,求函数
内的随机点,求函数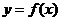 在区间
在区间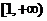
上是增函数的概率
解:(1)分别从集合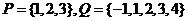 中随机取一个数作为
中随机取一个数作为 和
和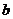 ,
,
共有不同组合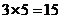 种,构成基本事件的总体个数,………2分
种,构成基本事件的总体个数,………2分
|
|
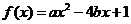 的对称轴
的对称轴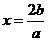 ,要使
,要使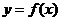 在区间
在区间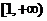 上是增函数,
上是增函数,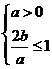 ,
, ,其中满足有5种,
,其中满足有5种,
所以所求事件的概率是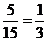 。
。
 (2)由(1)知当且仅当
(2)由(1)知当且仅当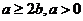 时,
时,
函数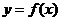 在区间
在区间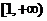 上是增函数,
上是增函数,
因为点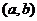 是区域
是区域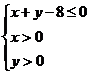 内的随机点,
内的随机点,
对应区域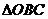 面积为
面积为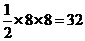 ,……9分
,……9分
函数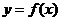 在区间
在区间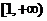 上是增函数满足的条件
上是增函数满足的条件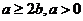 对应的区域
对应的区域
是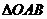 , 由
, 由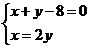 得交点
得交点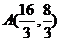 ,区域
,区域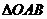 面积是
面积是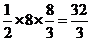
…………12分
所以所求事件的概率是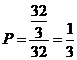 。…………14分
。…………14分
16.(本小题满分14分)
在 中,角
中,角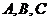 所对的边分别为
所对的边分别为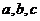 ,已知
,已知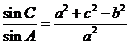 .
.
(1)求角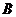 的大小; (2)设
的大小; (2)设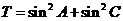 ,求
,求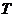 的取值范围.
的取值范围.
解:由正弦定理得 ,
,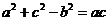 ,………3分
,………3分
由余弦定理得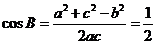 ,………5分
,………5分
又因为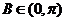 ,所以
,所以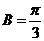 ;………7分
;………7分
(2)因为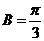 ,所以
,所以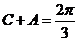 ,
,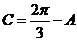 ,
,
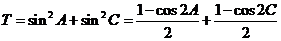
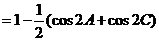
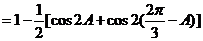
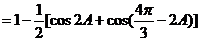
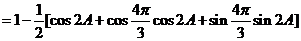
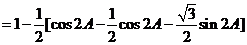
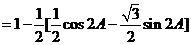
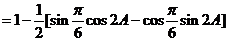
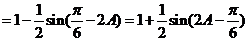
又因为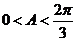 ,所以
,所以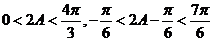 ,
,
∴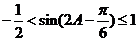 ,∴
,∴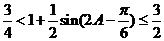 ,∴
,∴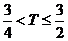 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com