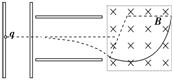
2．(2014·西安一中质检)如图8－3－18甲所示，竖直挡板MN的左侧空间有方向竖直向上的匀强电场和垂直纸面的水平匀强磁场，电场和磁场的范围足够大，电场强度的大小E＝40 N/C，磁感应强度B随时间t变化的关系图象如图乙所示，选定磁场垂直纸面向里为正方向，在t＝0时刻，一质量m＝8×10^－4 kg、带电荷量q＝＋2×10^－4 C的微粒在O点具有竖直向下的速度v＝0.12 m/s，O′是挡板MN上一点，直线OO′与挡板MN垂直，取g＝10 m/s².求：

图8－3－18

(1)微粒下一次经过直线OO′时到O点的距离．

(2)微粒在运动过程中离开直线OO′的最大距离．

(3)水平移动挡板，使微粒能垂直射到挡板上，挡板与O点间距离应满足的条件．

[解析]　(1)由题意知，微粒所受重力：

G＝mg＝8×10^－3 N

电场力大小为：F＝Eq＝8×10^－3 N

重力与电场力平衡，微粒先在洛伦兹作用下做匀速圆周运动，则有：qvB＝m

距O点的距离为：2R＝1.2 m

(2)微粒运动半周后向上匀速直线运动，运动时间为：

t＝5πs

轨迹如图所示：

故位移大小x＝vt＝0.6π m＝1.88 m

微粒离开直线OO′的最大距离：h＝x＋R＝2.48 m

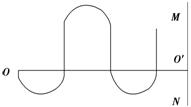
(3)若微粒能垂直射到挡板上的某点p，p点在直线OO′下方时，挡板MN与O点间的距离

应满足：L＝(4n＋1)×0.6 m　(n＝0、1、2、3…)

若微粒能垂直射到挡板上的某点p，p点在直线OO′上方时，挡板MN与O点间的距离应满足：

L＝(4n－1)×0.6 m　(n＝1、2、3…)

或L＝(4n＋3)×0.6 m　(n＝0、1、2、3…)

[答案]　(1)1.2 m　(2)2.48 m　(3)见解析

B组　高考题组

1.

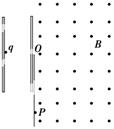
图8－3－17

(2014·北京朝阳区质检)如图8－3－17所示，一个静止的质量为m、电荷量为q的粒子(重力忽略不计)，经加速电压U加速后，垂直进入磁感应强度为B的匀强磁场中，粒子打到P点，OP＝x，能正确反映x与U之间关系的是(　)

A．x与U成正比

B．x与U成反比

C．x与成正比

D．x与成反比

[解析]　由x＝2R＝2mv/qB，qU＝mv²，可得x与成正比，选项C正确．

[答案]　C

2.

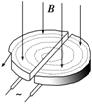
图8－3－14

(2013·济南一中检测)回旋加速器是加速带电粒子的装置．其主体部分是两个D形金属盒，两金属盒处于垂直于盒底的匀强磁场中，并分别与高频交流电源的两极相连接，从而使粒子每次经过两盒间的狭缝时都得到加速，如图

8－3－14所示．现要增大带电粒子从回旋加速器射出时的动能，下列方法可行的是(　)

A．增大金属盒的半径

B．减小狭缝间的距离

C．增大高频交流电压

D．减小磁场的磁感应强度

[解析]　选A.带电粒子射出时运动轨迹的半径等于D形盒的半径，设D形盒的半径为R，则有qvB＝m，最大动能mv²＝，显然增大金属盒的半径R、增大磁感应强度B均可以增大最大动能，A项正确．

[答案]　A

(对应学生用书第179页)

带电粒子在交变磁场中的运动

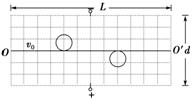
　如图8－3－15甲所示，互相平行且水平放置的金属板，板长L＝1.2 m，两板距离d＝0.6 m，两板间加上U＝0.12 V的恒定电压及随时间变化的磁场，磁场变化规律如图乙所示，规定磁场方向垂直纸面向里为正．当t＝0时，有一质量为m＝2.0×10^－6 kg、电荷量q＝＋1.0×10^－4 C的粒子从极板左侧以v₀＝4.0×10³ m/s的速度沿与两板平行的中线OO′射入，取g＝10 m/s²、π＝3.14.求：

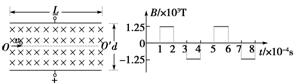
　　甲　　　　　乙

　图8－3－15

(1)粒子在0～1.0×10^－4 s内位移的大小x；

(2)粒子离开中线OO′的最大距离h；

(3)粒子在板间运动的时间t；

(4)画出粒子在板间运动的轨迹图．

[审题指导]　(1)粒子在0～1.0×10^－4 s内只受电场力和重力，当Eq＝mg时粒子做匀速直线运动．

(2)粒子离开中心线的最大距离为粒子圆周运动的直径．

(3)粒子在板间运动时间为圆周运动和直线运动时间之和．

[解析]　(1)由题意知：Eq＝q＝2.0×10^－5 N

而mg＝2.0×10^－5 N

显然Eq＝mg

故粒子在0～1.0×10^－4 s时间内做匀速直线运动，

因为Δt＝1.0×10^－4 s，

所以x＝v₀Δt＝0.4 m

(2)在1.0×10^－4～2.0×10^－4 s时间内，电场力与重力平衡，粒子做匀速圆周运动，

因为T＝＝1.0×10^－4 s

故粒子在1.0×10^－4～2.0×10^－4 s时间内恰好完成一个周期圆周运动

由牛顿第二定律得：

qv₀B＝　R＝＝0.064 m

h＝2R＝0.128 m<.

所以粒子离开中线OO′的最大距离h＝0.128 m.

(3)板长L＝1.2 m＝3x

t＝2T＋3Δt＝5.0×10^－4 s

(4)轨迹如图

[答案]　见解析

[即学即用]

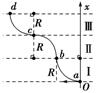
图8－3－16

　(2012·南京模拟)图8－3－16所示，一个质量为m、电荷量为＋q的带电粒子，不计重力，在a点以某一初速度水平向左射入磁场区域Ⅰ，沿曲线abcd运动，ab、bc、cd都是半径为R的圆弧，粒子在每段圆弧上运动的时间都为t.规定垂直于纸面向外的磁感应强度为正，则磁场区域Ⅰ、Ⅱ、Ⅲ三部分的磁感应强度B随x变化的关系可能是下列中的(　)

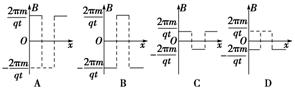
[解析]　由左手定则可判断出磁感应强度B在磁场区域Ⅰ、Ⅱ、Ⅲ内磁场方向分别为向外、向里和向外，在三个区域中均运动1/4圆周，故t＝T/4，由于T＝，求得B＝，只有选项C正确．

[答案]　C

(对应学生用书第179页)

A组　双基题组

1．(2013·北京朝阳区质检)如图8－3－12所示，一个质量m＝2.0×10^－11 kg、电荷量q＝1.0×10^－5 C的带电粒子(重力忽略不计)，从静止开始经U₁＝100 V电场加速后，沿两平行金属板间中线水平进入电压U₂＝100 V的偏转电场，带电粒子从偏转电场射出后，进入垂直纸面向里的匀强磁场，磁场的左右边界均与偏转电场的金属板垂直．已知偏转电场金属板长L＝20 cm，两板间距d＝10 cm，匀强磁场的宽度D＝10 cm.求：

(1)带电粒子进入偏转电场时的速度v₀；

(2)带电粒子射出偏转电场时速度v的大小；

(3)为了使带电粒子不从磁场右边界射出，匀强磁场磁感应强度的最小值B.

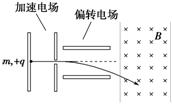
图8－3－12

[解析]　(1)带电粒子在加速电场中加速，由动能定理：

　qU₁＝mv

解得：v₀＝1.0×10⁴ m/s.

(2)带电粒子在偏转电场中做水平方向的匀速直线运动和坚直方向的匀加速直线运动．

则a＝

v_y＝at＝a

飞出电场时，速度偏转角的正切值为：tan θ＝＝＝，θ＝30°

带电粒子射出偏转电场时速度的大小：v＝＝×10⁴ m/s≈1.15×10⁴ m/s.

(3)带电粒子不从磁场右边界射出，则其最大半径的运动轨迹如图所示，设带电粒子在磁场中运动的最大半径为r，由几何关系有：D＝r＋rsin θ

洛伦兹力提供向心力：qvB＝

联立可得：B＝

代入数据：B＝T≈0.346 T

[答案]　(1)1.0×10⁴ m/s　(2)1.15×10⁴ m/s

(3)0.346 T

回旋加速器的原理和应用

回旋加速器中带电粒子运动的周期与高频电压的周期相同，周期的大小不随粒子速度的变化而变化．粒子获得的最大动能与D形盒的最大半径有关，与加速电压、加速次数等无关．

　(多选)(2013·河南省实验中学模拟)图8－3－13甲是回旋加速器的原理示意图．其核心部分是两个D形金属盒，在加速带电粒子时，两金属盒置于匀强磁场中(磁感应强度大小恒定)，并分别与高频电源相连．加速时某带电粒子的动能E_k随时间t的变化规律如图乙所示，若忽略带电粒子在电场中的加速时间，则下列判断正确的是(　)

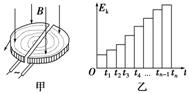
图8－3－13

A．在E_k－t图象中t₄－t₃＝t₃－t₂＝t₂－t₁

B．高频电流的变化周期应该等于t_n－t_n－1

C．粒子加速次数越多，粒子获得的最大动能一定越大

D．D形盒的半径越大，粒子获得的最大动能越大

[解析]　粒子在磁场中运动的周期T＝，与粒子的速度无关，粒子每次在D形盒内运动半个周期的时间都相等，故t₄－t₃＝t₃－t₂＝t₂－t₁，A对；高频电流的变化周期与粒子在磁场中运动的周期相等，但粒子每周期要进行两次加速，故T＝2(t_n－t_n－1)，B错；粒子最大动能与加速次数无关，C错；根据qvB＝可推出E_km＝.R越大，E_km越大，D对．

[答案]　AD

[迁移应用]

3．带电粒子在磁场中的运动要根据磁场的边界条件，几何关系和圆周运动知识解答．

　(2013·安徽高考)如图8－3－11所示的平面直角坐标系xOy，在第Ⅰ象限内有平行于y轴的匀强电场，方向沿y轴正方向；在第Ⅳ象限的正三角形abc区域内有匀强磁场，方向垂直于xOy平面向里，正三角形边长为L，且ab边与y轴平行．一质量为m、电荷量为q的粒子，从y轴上的P(0，h)点，以大小为v₀的速度沿x轴正方向射入电场，通过电场后从x轴上的a(2h,0)点进入第Ⅳ象限，又经过磁场从y轴上的某点进入第Ⅲ象限，且速度与y轴负方向成45°角，不计粒子所受的重力．求：

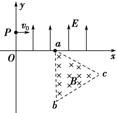
图8－3－11

(1)电场强度E的大小；

(2)粒子到达a点时速度的大小和方向；

(3)abc区域内磁场的磁感应强度B的最小值．

[审题指导]　

[解析]　带电粒子在电场中做类平抛运动，在磁场中做匀速圆周运动，射出磁场后做匀速直线运动．

(1)带电粒子在电场中从P到a的过程中做类平抛运动

水平方向上：2h＝v₀t①

竖直方向上：h＝at²②

由牛顿第二定律得a＝③

由①②③式联立，解得E＝④

(2)粒子到达a点时沿y轴负方向的分速度为v_y＝at⑤

由①③④⑤式得v_y＝v₀⑥

而v_x＝v₀⑦

粒子到达a点的速度v_a＝＝v₀⑧

设速度方向与x轴正方向的夹角为θ，则tan θ＝＝1，θ＝45°⑨

即到a点时速度方向指向第Ⅳ象限与x轴正方向成45°角．

(3)粒子进入磁场后做匀速圆周运动，有qvB＝m⑩

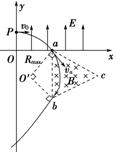
由此得R＝⑪

从上式看出，R∝，当R最大时，B最小．

由题图可知，当粒子从b点射出磁场时，R最大

由几何关系得R_max＝L⑫

将⑫代入⑪式得B的最小值为B_min＝.

[答案]　(1)　(2)v₀　方向指向第Ⅳ象限与x轴正方向成45°角

(3)

[迁移应用]

2．带电粒子在电场中运动一般分为两种情况

(1)加速：根据动能定理，有qU＝mv－mv.

(2)偏转：根据类平抛运动的解题方法．

1.组合场具有阶段性，解答问题时要根据粒子所处的不同场中受力情况，运动情况的不同，分别选择不同的运动规律解题．

4．(2013·长沙一中检测)如图8－3－10所示，水平放置的平行金属板a、b带有等量正负电荷，a板带正电，两板间有垂直于纸面向里的匀强磁场，一个带正电的粒子在两板间做直线运动，粒子的重力不计．关于粒子在两板间运动的情况，正确的是(　)

A．可能向右做匀加速直线运动

B．可能向左做匀加速直线运动

C．只能是向右做匀速直线运动

D．只能是向左做匀速直线运动

[解析]　经受力分析可知电场力向下，洛伦兹力必向上，则速度向右；洛伦兹力与速度大小有关，因此只能为匀速直线运动．

[答案]　C

(对应学生用书第177页)

带电粒子在组合场中的运动

3.

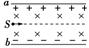
图8－3－9

如图8－3－9所示，a、b是位于真空中的平行金属板，a板带正电，b板带负电，两板之间的电场为匀强电场，场强为E.同时在两板之间的空间中加匀强磁场，磁场方向垂直于纸面向里，磁感应强度为B.一束电子以大小为v₀的速度从左边S处沿图中虚线方向入射，虚线平行于两板．要想使电子在两板间能沿虚线运动，则v₀、E、B之间的关系应该是(　)

A．v₀＝　　　　　　　　　　　　　　　　　　　　　　　　　 B．v₀＝

C．v₀＝ 　 D．v₀＝

[解析]　电子沿直线运动时，必有Eq＝Bv₀q，故v₀＝，A正确．

[答案]　A

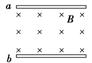
图8－3－10

2.

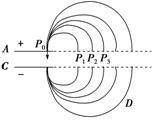
图8－3－8

(2014·武汉一中质检)美国物理学家劳伦斯于1932年发明的回旋加速器，应用带电粒子在磁场中做圆周运动的特点，能使粒子在较小的空间范围内经过电场的多次加速获得较大的能量，使人类在获得以较高能量带电粒子方面前进了一步，如图8－3－8所示为一种改进后的回旋加速器示意图，其中盒缝间的加速电场场强大小恒定，且被限制在A、C板间，带电粒子从P₀处静止释放，并沿电场线方向射入加速电场，经加速后再进入D形盒中的匀强磁场做匀速圆周运动，对于这种改进后的回旋加速器，下列说法正确的是(　)

A．带电粒子每运动一周被加速一次

B．P₁P₂＝P₂P₃

C．加速粒子的最大速度与D形盒的尺寸无关

D．加速电场方向需要做周期性的变化

[解析]　带电粒子每运动一周被加速一次，加速电场方向不需要做周期性的变化，选项A正确，D错误．由nqU＝ mv，r_n＝mv_n/qB解得r_n＝/qB，由此可知，P₁P₂≠P₂P₃，选项B错误．由v＝知选项C错误．

[答案]　A