5．(多选)(2013·四川高考)甲、乙两物体在t＝0时刻经过同一位置沿x轴运动，其v－t图象如图1－3－10所示，则

(　)

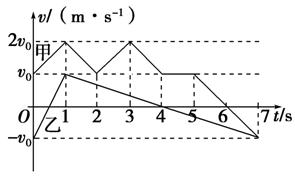
图1－3－10

A．甲、乙在t＝0到t＝1 s之间沿同一方向运动

B．乙在t＝0到t＝7 s之间的位移为零

C．甲在t＝0到t＝4 s之间做往复运动

D．甲、乙在t＝6 s时的加速度方向相同

[解析]　速度图象中坐标的正负表示物体的速度方向，即物体的运动方向，故A错误；速度图象与时间轴所围面积表示物体的位移，由题图知在0～7 s内乙物体速度图线与时间轴所围总面积为零，故B正确．在0～4 s内甲物体的速度始终为正，即这段时间内一直沿正方向运动，故C错误；速度图线的斜率表示加速度，即斜率绝对值表示加速度的大小，斜率的正负表示加速度的方向，由题图可知D正确．

[答案]　BD

4. (多选)(2013·新课标全国卷Ⅰ)如图1－3－9，直线a和曲线b分别是在平直公路上行驶的汽车a和b的位置－时间(x－t)图线．由图可知(　)

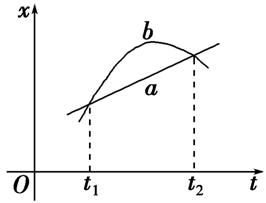
图1－3－9

A．在时刻t₁，a车追上b车

B．在时刻t₂，a、b两车运动方向相反

C．在t₁到t₂这段时间内，b车的速率先减少后增加

D．在t₁到t₂这段时间内，b车的速率一直比a车的大

[解析]　t₁时刻前b处于a的后方，该时刻应是b车追上a车，A错；t₂时刻b车沿－x方向运动，a车沿＋x方向运动，B对；x－t图线的斜率大小表示速率，由t₁－t₂时间内b车图线的斜率变化知，C对；在b车图线的顶点处切线水平，表示v_b＝0，故D错．

[答案]　BC

3．甲、乙两运动员在训练交接棒的过程中发现：甲经短距离加速后能保持9 m/s的速度跑完全程，乙从起跑后到接棒前的运动是匀加速的．为了确定乙起跑的时机，需在接力区前适当的位置设置标记．在某次练习中，甲在接力区前s₀＝13.5 m处作了标记，并以v＝9 m/s的速度跑到此标记时向乙发出起跑口令．乙在接力区的前端听到口令时起跑，并恰好在速度达到与甲相同时被甲追上，完成交接棒．已知接力区的长度为L＝20 m，求：

(1)求此练习中乙在接棒前的加速度a.

(2)在完成交接棒时乙离接力区末端的距离．

[解析]　根据题意可画出甲、乙二人的运动示意图如下：

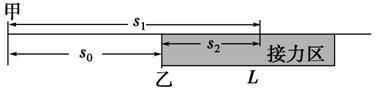
(1)在甲发出口令后到甲、乙达到共同速度所用时间为

t＝　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ①

设在这段时间内甲、乙的位移分别为s₁和s₂则

s₂＝at² ②

s₁＝vt　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ③

s₁＝s₂＋s₀ ④

联立①②③④式解得a＝，即a＝3 m/s².

(2)在这段时间内，乙在接力区的位移为s₂＝，得s₂＝13.5 m.

完成交接棒时，乙与接力区末端的距离为L－s₂＝6.5 m.

[答案]　(1)3 m/s²　(2)6.5 m

B组　高考题组

2．(多选)下列图象能正确反映物体在直线上运动，经2 s一定回到初始位置的是(　)

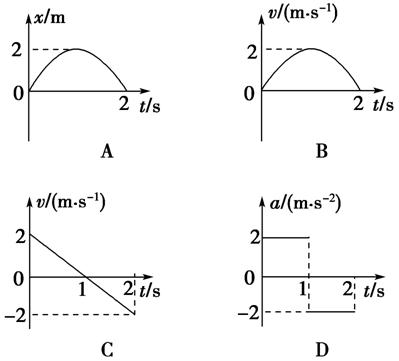
[解析]　由x－t图象可以看出A选项正确．在v－t图象中，图象和坐标轴包围的面积在数值上等于位移的大小，所以C项正确，B项不正确．在D图象中，若物体速度与加速度同向，则始终朝同一方向运动，因此位移不能为零，故D选项不正确．

[答案]　AC

1．两辆游戏赛车a、b在两条平行的直车道上行驶，t＝0时两车都在同一计时线处，此时比赛开始．它们在四次比赛中的v－t图象如图所示．哪些图象对应的比赛中，有一辆赛车追上了另一辆(　)

[解析]　由v－t图象的特点可知，图线与t轴所围面积的大小，即为物体位移的大小．观察4个图象，只有C选项中，a、b所围面积的大小有相等的时刻，故选项C正确．

[答案]　C

3．甲车以10 m/s的速度在平直的公路上匀速行驶，乙车以4 m/s的速度与甲车平行同向做匀速直线运动，甲车经过乙车旁边开始以0.5 m/s²的加速度刹车，从甲车刹车开始计时，求：

(1)乙车在追上甲车前，两车相距的最大距离；

(2)乙车追上甲车所用的时间．

[解析]　(1)当甲车速度减至等于乙车速度时两车的距离最大，设该减速过程经过的时间为t，则

v_乙＝v_甲－at

解得：t＝12 s

此时甲乙间的距离为

Δx＝v_甲t－at²－v_乙t

＝10×12 m－×0.5×12² m－4×12 m＝36 m.

(2)设甲车减速到零所需时间为t₁，则有：t₁＝＝20 s

t₁时间内：x_甲＝t₁＝×20 m＝100 m

x_乙＝v_乙t₁＝4×20 m＝80 m

此后乙车运动时间：t₂＝＝ s＝5 s

故乙车追上甲车需t₁＋t₂＝25 s.

[答案]　(1)36 m　(2)25 s

利用运动图象分析相遇问题

利用图象分析追及、相遇问题，是常见的物理模型，以下是利用v－t图象分析这类问题的要点．

(1)由斜率分析、计算加速度．

(2)由“面积”求位移．

(3)由运动性质和“相对位移”变化(看图线走势)判断相遇(或距离最大)时刻．

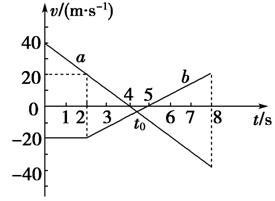
图1－3－8

　如图1－3－8所示，a、b分别是甲、乙两辆车从同一地点沿同一直线同时运动的v－t图线，由图线可以判断

(　)

A．2秒后甲、乙两车的加速度大小相等

B．在0～8 s内两车最远相距148 m

C．两车只有t₀时刻速率相等

D．两车在t＝8 s时相遇

[审题指导]　(1)由图象斜率可比较加速度大小．

(2)由图象信息可知a、b开始时是向相反方向运动的，4 s时a反向，至t₀时刻二者速度相同，此时，二者应相距最远，之后a速度大于b的速度，5 s后b反向与a相向运动，二者越来越近．

(3)a、b是同地同时出发，图中信息显示8 s时，a回到出发点，此时二者是否相遇，要看b是否回到出发点．

[解析]　2秒后a_甲＝ m/s²＝－10 m/s²，a_乙＝ m/s²＝ m/s²，所以两车加速度大小不等，A错．由题图可知两车在0～8 s内相距最远应在两车速度相等，即t₀时刻，由a、b两直线可求出t₀＝4.4 s，则两车相距最远距离应为a、b两线和纵轴围成的面积，解得x＝148 m，故B对．除t₀外，t＝2 s时，两车速率也相等，C错．t＝8 s时，甲返回到出发点．乙在负方向40 m，故未相遇，D错．

[答案]　B

用图象法解决追及、相遇问题时

应把握的三个环节

(1)画图：定量画图时需根据物体在不同阶段的运动情况，通过定量计算分阶段、分区间逐一描图．

(2)转换图：从不同的角度描绘同一物理过程所进行的变换，如将x－t图象转换成v－t图象等．

(3)用图：利用图象中斜率、面积、截距、交点等的含义进行定性分析或定量计算，进而解决相关问题．

[即学即用]

两辆完全相同的汽车，沿水平路面一前一后均以20 m/s的速度前进．若前车突然以恒定的加速度刹车，在它刚停止时，后车以前车刹车时的加速度的2倍开始刹车．已知前车刹车的过程中所行驶的距离为100 m，若要保证两车在上述情况下不相撞，则两车在匀速行驶时保持的最小距离是多少？

[解析]　设前、后两车的加速度分别为a₁、a₂，从刹车开始到停止所用的时间分别为t₁、t₂.由题意知，a₂＝2a₁，则t₂＝t₁，根据题意作出两车从前车刹车开始的v－t图象，分别为AC和ABD.

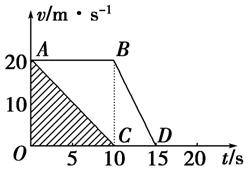
图中三角形AOC的面积为前车刹车后的位移，且x₁＝100 m，梯形ABDO为从前车刹车后后车的位移，由图象可知，矩形ABCO面积为三角形AOC面积的二倍，三角形BCD面积为三角形AOC面积的，即梯形ABDO面积为三角形AOC面积的2.5倍．由此得，后车从前车刹车开始到自己停止通过的距离为x₂＝250 m，因此为使两车不相撞，两车在匀速行驶时应保持的最小距离为：Δx＝x₂－x₁＝150 m.

[答案]　150 m

A组　双基题组

2．解题思路和方法

—→—→—→

　A、B两列火车，在同一轨道上同向行驶，A车在前，其速度v_A＝10 m/s，B车在后，速度v_B＝30 m/s，因大雾能见度很低，B车在距A车x₀＝75 m时才发现前方有A车，这时B车立即刹车，但B车要经过180 m才能停止，问：B车刹车时A车仍按原速率行驶，两车是否会相撞？若会相撞，将在B车刹车后多长时间相撞？若不会相撞，则两车最近距离是多少？

[解析]　B车刹车至停下来的过程中，由v²－v＝2ax得a_B＝＝－2.5 m/s²

解法一　物理分析法

假设不相撞，依题意画出运动过程示意图，如下图所示．

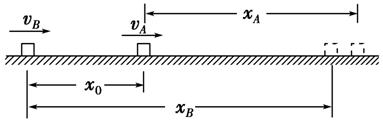
设经过时间t两车速度相等，对B车有：v_A＝v_B＋a_Bt

解得t＝＝8 s.

此时B车的位移x_B＝v_Bt＋a_Bt²＝30×8 m－×2.5×8² m＝160 m.

A车的位移x_A＝v_At＝10×8 m＝80 m.

因x_B>x_A＋x₀，故两车会相撞．

设B刹车后经过时间t_x两车相撞，则有v_At_x＋x₀＝v_Bt_x＋a_Bt，

代入数据解得，t_x＝6 s或t_x＝10 s(舍去)．

解法二　图象法

由上可知a_B＝－2.5 m/s²，作出A、B两车运动的速度时间图象如下图，则由图象可知8 s时二者速度相等，则可得两车在8 s内的位移分别为：

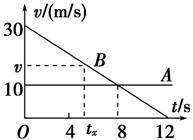
x_B＝×(30＋10)×8 m＝160 m，

x_A＝10×8 m＝80 m.

因x_B>x_A＋x₀，故两车会相撞．

设经过时间t_x两车相撞，如图此时B车的速度为v，则有×(30＋v)t_x＝10t_x＋x₀，

由几何关系得：＝，

联立解得，t_x＝6 s或t_x＝10 s(舍去)．

解法三　数学分析法

设B车刹车后经过时间t_x两车相撞，则A、B两车发生的位移关系为：x_B＝x_A＋x₀.

其中x_B＝v_Bt＋a_Bt²，x_A＝v_At，

代入整理得：2.5t²－40t＋150＝0.

判别式Δ＝b²－4ac＝(－40)²－4×2.5×150＝100>0，则方程有解，两车会相撞，解得：t_x＝6 s或t_x＝10 s(舍去)．

[答案]　会相撞　6 s

解答追及、相遇问题的常用方法

(1)物理分析法：应用运动学公式，根据每个物体的运动情况，分别确定出各物体间的位移、时间和速度关系，并列出方程，进行求解．

(2)相对运动法：巧妙地选取参考系，然后找两物体的运动关系．

(3)极值法：设相遇时间为t，根据条件列方程，得到关于t的一元二次方程，用判别式进行讨论．若Δ>0，即有两个解，说明可以相遇两次，若Δ＝0，说明刚好追上或相碰；若Δ<0，说明追不上或不能相碰．

(4)图象法：将两者的v－t图象在同一个坐标系中画出，然后利用图象求解．

[迁移应用]

1.讨论追及、相遇的问题，其实质就是分析讨论两物体在相同时间内能否到达相同空间位置的问题

(1)两个关系：即时间关系和位移关系，这两个关系可通过画草图得到．

(2)一个条件：即两者速度相等，它往往是物体间能否追上、追不上或(两者)距离最大、最小的临界条件，也是分析判断的切入点．

2．如图1－3－7所示的位移—时间图象和速度—时间图象中，给出四条图线1、2、3、4代表四个不同物体的运动情况，关于它们的物理意义，下列描述正确的是(　)

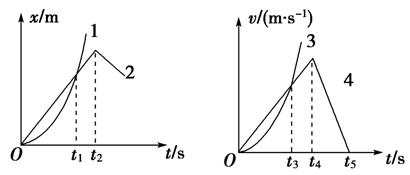
图1－3－7

A．图线1表示物体做曲线运动

B. x－t图象中t₁时刻v₁＞v₂

C. v－t图象中0至t₃时间内3和4的平均速度大小相等

D．两图象中，t₂、t₄时刻分别表示2、4开始反向运动

[解析]　图线1是位移图象，表示物体是做变速直线运动，所以选项A错；x－t图线上某点斜率的绝对值表示速度的大小，选项B正确；v－t图象中0至t₃时间内3和4位移不同，所以平均速度不相等，选项C错；t₂时刻2开始反向运动，t₄时刻4加速度方向变化但运动方向不变，所以选项D错．

[答案]　B

追及、相遇问题的分析

1.(多选)甲、乙两物体由同一位置出发沿同一直线运动，其速度——时间图象如图1－3－6所示，下列说法正确的是

(　)

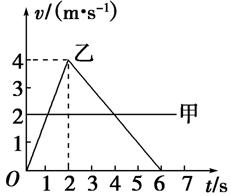
图1－3－6

A．甲做匀速直线运动，乙做匀变速直线运动

B．两物体两次相遇的时刻分别是在2 s末和6 s末

C．乙在前2 s内做匀加速直线运动，2 s后做匀减速直线运动

D．2 s后，甲、乙两物体的速度方向相反

[解析]　由图象知，v_甲＝2 m/s，故甲物体做匀速直线运动，乙物体在0～2 s内沿正方向做匀加速直线运动．在2～6 s内沿正方向做匀减速直线运动，乙物体在整个过程中做的不是匀变速直线运动，A错误，C正确；在2 s末，甲物体的位移x_甲＝2×2 m＝4 m，乙物体的位移x_乙＝×(2×4) m＝4 m，故两物体在2 s末相遇，在6 s末，甲物体的位移x_甲′＝2×6 m＝12 m，乙物体的位移x_乙′＝ × (6×4) m＝12 m，故两物体在6 s末相遇，B正确；在0～6 s内，甲、乙两物体始终沿规定的正方向运动，D错误．

[答案]　BC

●x－t图线与v－t图线的比较