
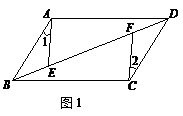
7.如图 ,平行四边形
,平行四边形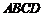 中,
中,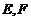 是对角线
是对角线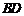 上的两点,如果添加一个条件使
上的两点,如果添加一个条件使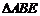 ≌
≌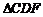 ,则添加的条件不能是
,则添加的条件不能是
 A.
A.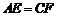 B.
B.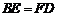 C.
C. 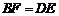 D.
D.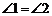
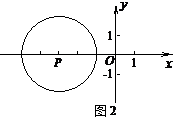
6.正比例函数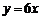 的图象与反比例函数
的图象与反比例函数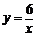 的图象的交点位于
的图象的交点位于
A.第一象限 B.第二象限
B.第二象限
C.第三象限 D.第一、三象限
5.一 元二次方程
元二次方程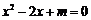 总有实数根,则
总有实数根,则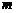 应满足的条件是
应满足的条件是
A.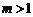 B.
B.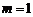 C.
C.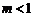 D.
D.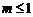
4.下列图形中,既是轴对称图形又是中心对称图形的是

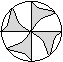


A B C D
3.小玲在一次班会中参与知识抢答活动,现有语文题6个,数学题5个,综合题9个,她从中随机抽取1个,抽中数学题的概率是
A.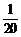 B
B .
.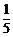 C.
C.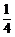 D.
D.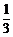
2.下列式子化简后的结果为 的是
的是
A.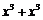 B.
B.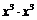 C.
C.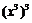 D.
D. 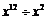
一、选择题
1.四个实数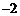 ,
,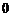 ,
,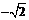 ,
,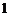 中,最大的实数是
中,最大的实数是
A.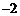 B.
B.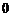 C.
C.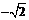 D.
D.
三、解答题
17.(2014四川南充,17,6分)计算: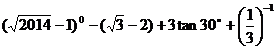
[答案]解: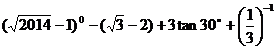
=1-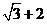 +3
+3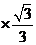 +
+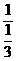 =1-
=1-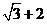 +
+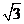 +3=6
+3=6
18. (2014四川南充,18,8分)如图,AD、BC相交于O,OA=OC,∠OBD=∠ODB.
 求证:AB=CD.
求证:AB=CD.
[答案]证明:∵∠OBD=∠ODB.
∴OB=OD
在△AOB与△COD中,
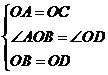
∴△AOB≌△COD(SAS)
∴AB=CD.
19.(2014四川南充,19,8分)(8分)在学习“二元一次方程组的解”时,数学张老师设计了一个数学活动. 有A、B 两组卡片,每组各3张,A组卡片上分别写有0,2,3;B组卡片上分别写有-5,-1,1.每张卡片除正面写有不同数字外,其余均相同.甲从A组中随机抽取一张记为x,乙从B组中随机抽取一张记为y.
(1)若甲抽出的数字是2,乙抽出的数是-1,它们恰好是ax-y=5的解,求a的值;
(2)求甲、乙随机抽取一次的数恰好是方程ax-y=5的解的概率.(请用树形图或列表法求解)
[答案]解:
20. (2014四川南充,20,8分)(8分)已知关于x的一元二次方程x2-2x+m=0,有两个不相等的实数根.
⑴求实数m的最大整数值;
⑵在⑴的条下,方程的实数根是x1,x2,求代数式x12+x22-x1x2的值.
[答案]解:⑴由题意,得:△>0,即: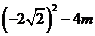 >0,m<2,∴m的最大整数值为m=1
>0,m<2,∴m的最大整数值为m=1
(2)把m=1代入关于x的一元二次方程x2-2x+m=0得x2-2x+1=0,根据根与系数的关系:x1+x2 = 2,x1x2=1,∴x12+x22-x1x2= (x1+x2)2-3x1x2=(2)2-3×1=5
21.(2014四川南充,21,8分)(8分)如图,一次函数y1=kx+b的图象与反比例函数y2=的图象相交于点A(2,5)和点B,与y轴相交于点C(0,7).
(1)求这两个函数的解析式;
(2)当x取何值时,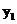 <
<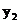 .
.
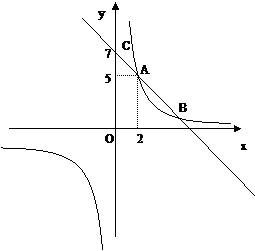
(第21题图)
[答案]解:∵反比例函数y2=的图象过点A(2,5)
∴5=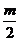 ,m=10
,m=10
即反比例函数的解析式为y=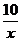 。
。
∵一次函数y1=kx+b的图象过A(2,5)和C(0,7).
∴5=2k+7,k= -1
即一次函数解析式为y=-x+7
(2)解方程组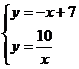 得
得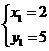 或
或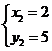
∴另一交点B的坐标为(5,2).
根据图象可知,当x<2或x>5时,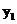 <
<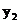 .
.
22. (2014四川南充,22,8分)(8分)马航MH370失联后,我国政府积极参与搜救.某日,我两艘专业救助船A、B同时收到有关可疑漂浮物的讯息,可疑漂浮物P在救助船A的北偏东53.50方向上,在救助船B的西北方向上,船B在船A正东方向140海里处。(参考数据:sin36.5≈0.6,cos36.5≈0.8,tan36.5≈0.75).
(1)求可疑漂浮物P到A、B两船所在直线的距离;
(2)若救助船A、救助船B分别以40海里/时,30海里/时的速度同时出发,匀速直线前往搜救,试通过计算判断哪艘船先到达P处。
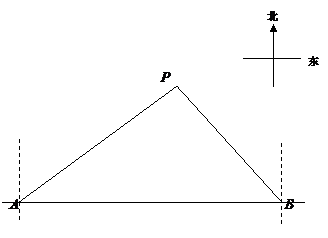
(第22题图)
[答案]解:(1)如图,过点P作PH⊥AB于点H,则PH的长是P到A、B两船所在直线的距离.
根据题意,得∠PAH=90°-53.50°=36.5°,∠PBH=45°,AB=140海里.
设PH=x海里
在Rt△PHB中,tan45°=,∴BH=x;
在Rt△PHA中,tan36.5°=,∴AH==x.∵AB=140,∴x +x=140,解得x=60,即PH=60,因此可疑漂浮物P到A、B两船所在直线的距离为60海里.
(2)在Rt△PHA中,AH=×60=80, PA==100,救助船A到达P处的时间tA=100÷40=2.5小时;在Rt△PHB中,PB==60,救助船B到达P处的时间tB=60÷30=2小时.
∵2.5<2,∴救助船A先到达P处.

23、(2014四川南充,23,8分)(8分)今年我市水果大丰收,A、B两个水果基地分别收获水果380件、320件,现需把这些水果全部运往甲、乙两销售点,从A基地运往甲、乙两销售点的费用分别为每件40元和20元,从B基础运往甲、乙两销售点的费用分别为每件15元和30元,现甲销售点需要水果400件,乙销售点需要水果300件。
(1)设从A基础运往甲 销售点水果x件,总运费为w元,请用含x的代数式表示w,并写出x的取值范围;
(2)若总运费不超过18300元,且A地运往甲销售点的水果不低于200件,试确定运费最低的运输方案,并求出最低运费。
[答案]解:(1)依题意,列表得
|
|
A(380) |
B(320) |
|
甲(400) |
x |
400-x |
|
乙(300) |
380-x |
320-(400-x)=x-80 |
∴W=40x+20×(380-x)+15×(400-x)+30×(x-80)=35x+11200
又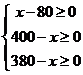 解得80≤x≤380
解得80≤x≤380
(2) 依题意得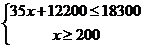 解得
解得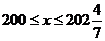 ,∴x=200,201,202
,∴x=200,201,202
因w=35x+10,k=35,w随x的增大而增大,所以x=200时,运费w最低,最低运费为81200元。
此时运输方案如下:
|
|
A |
B |
|
甲 |
200 |
200 |
|
乙 |
180 |
120 |
24. (2014四川南充,24,8分)如图,已知AB是⊙O的直径,BP是⊙O的弦,弦CD⊥AB于点F,交BP于点G,E在CD的延长线上,EP=EG,
(1)求证:直线EP为⊙O的切线;
(2)点P在劣弧AC上运动,其他条件不变,若BG²=BF·BO.试证明BG=PG.
(3)在满足(2)的条件下,已知⊙O的半径为3,sinB=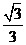 .求弦CD的长.
.求弦CD的长.

(第24题图)
[答案]解:
25. (2014四川南充,25,10分)如图,抛物线y=x²+bx+c与直线y=x-1交于A、B两点.点A的横坐标为-3,点B在y轴上,点P是y轴左侧抛物线上的一动点,横坐标为m,过点P作PC⊥x轴于C,交直线AB于D.
(1)求抛物线的解析式;
(2)当m为何值时,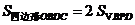 ;
;
(3)是否存在点P,使△PAD是直角三角形,若存在,求出点P的坐标;若不存在,说明理由.

[答案]解:
1)由已知得,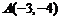 ,
,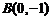 ,
,
∴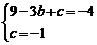 ,
,
解得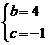 ,
,
∴  .
.
(2)∵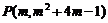 ,
,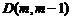 ,
,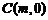
∴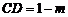 .
.
∵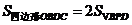 ,即
,即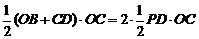 ,∴
,∴ .
.
当点P运动至A处,此时P、D重合.
① 当PD在点A左侧时,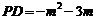 ,则
,则 ,
,
解得,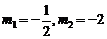 .
.
② 当PD在点A右侧时,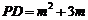 ,则
,则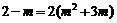 ,
,
解得,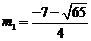 ,
,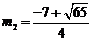 不合题意,舍去.
不合题意,舍去.
综上,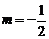 ,
,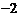 或
或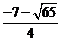 .
.
(3)∵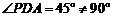 ,∴当
,∴当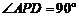 或
或 时,△PAD是直角三角形.
时,△PAD是直角三角形.
① 若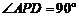 ,则AP∥x轴,∴
,则AP∥x轴,∴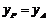 ,即
,即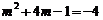 ,
,
解得,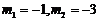 ,∴
,∴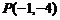 ;
;
② 若 ,AP⊥AB.
,AP⊥AB.
又直线AP: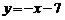 ,
,
由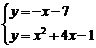 ,解得
,解得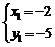 ,
,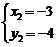 ,∴
,∴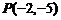 .
.
综上,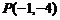 或
或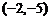 .
.
二、填空题
11.(2014四川南充,11,3分)分式方程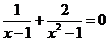 的解是__________.
的解是__________.
[答案]x= -3
12.(2014四川南充,12,3分)因式分解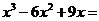 __________.
__________.
[答案]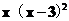
13.(2014四川南充,13,3分)一组数据按从小到大的顺序排列为1,2,3,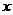 ,4,5,若这组数据的中位数为3,则这组数据的方差是__________.
,4,5,若这组数据的中位数为3,则这组数据的方差是__________.
[答案]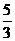
14.(2014四川南充,14,3分)如图,两圆圆心相同,大圆的弦AB与小圆相切,AB=8,则图中阴影部分的面积是__________.(结果保留π)
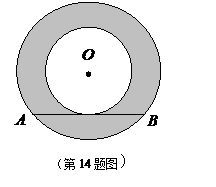
[答案]16π
15. (2014四川南充,15,3分)一列数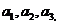 ……
……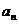 ,其中
,其中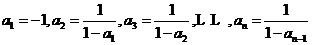 ,则
,则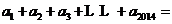 __________.
__________.
[答案]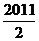
16.(2014四川南充,16,3分)如图,有一矩形纸片ABCD,AB=8,AD=17,将此矩形纸片折叠,使顶点A落在BC边的A′处,折痕所在直线同时经过边AB、AD(包括端点),设BA′=x,则x的取值范围是 .

[答案]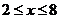
一、选择题
1.(2014四川南充,1,3分)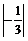 的值是( )
的值是( )
A.3 B.-3 C. D.-
[答案]C
2.(2014四川南充,2,3分)下列运算正确的是( )
A.a3a2=a5 B.(a2) 3=a5 C.a3+a3=a6 D.(a+b)2=a2+b2
[答案]A
3.(2014四川南充,3,3分)下列几何体的主视图既是中心对称图形又是轴对称图形的是( )
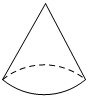

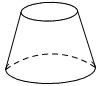
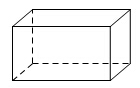
A B C D
[答案]D
4.(2014四川南充,4,3分)如图,已知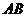 ∥
∥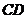 ,
,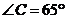 ,
,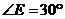 ,则
,则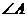 的度数为( )
的度数为( )

(第2题图)
A.30° B.32.5° C.35° D.37.5°
[答案]C
5.(2014四川南充,5,3分)如图,将正方形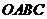 放在平面直角坐标系中,
放在平面直角坐标系中,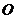 是原点,
是原点,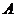 的坐标为(1,
的坐标为(1,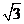 ),则点
),则点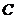 的坐标为( )
的坐标为( )
(第5题图)
A.(-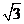 ,1) B.(-1,
,1) B.(-1,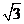 ) C.(
) C.(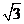 ,1) D.(-
,1) D.(-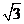 ,-1)
,-1)
[答案]A
6.(2014四川南充,6,3分)不等式组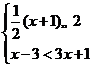 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
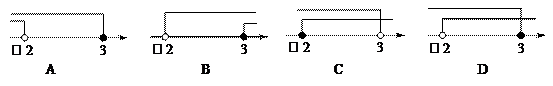
[答案]D
7.(2014四川南充,7,3分)为积极响应南充市创建“全国卫生城市”的号召,某校1 500名学生参加了卫生知识竞赛,成绩记为A、B、C、D四等。从中随机抽取了部分学生成绩进行统计,绘制成如下两幅不完整的统计图表,根据图表信息,以下说法不正确的是( )

A.样本容量是200 B.D等所在扇形的圆心角为15°
C.样本中C等所占百分比是10% D.估计全校学生成绩为A等大约有900人
[答案]B
8.(2014四川南充,8,3分)如图,在△ABC中,AB=AC,且D为BC上一点,CD=AD,AB=BD,则∠B的度数为( )
A.30° B.36° C.40° D.45°
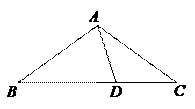
(第8题图)
[答案]B
9.(2014四川南充,9,3分)如图,矩形ABCD中,AB=5,AD=12,将矩形ABCD按如图所示的方式在直线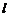 上进行两次旋转,则点B在两次旋转过程中经过的路径的长是( )
上进行两次旋转,则点B在两次旋转过程中经过的路径的长是( )
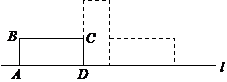
(第9题图)
A.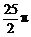 B.
B.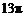 C.
C.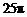 D.
D.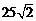
[答案]B
10.(2014四川南充,10,3分)二次函数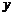 =
=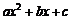 (
(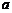 ≠0)图象如图所示,下列结论:①
≠0)图象如图所示,下列结论:①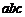 >0;②
>0;②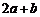 =0;③当
=0;③当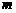 ≠1时,
≠1时,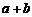 >
>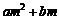 ;④
;④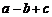 >0;⑤若
>0;⑤若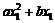 =
=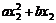 ,且
,且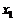 ≠
≠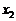 ,则
,则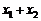 =2.其中正确的有( )
=2.其中正确的有( )
A.①②③ B.②④ C.②⑤ D.②③⑤
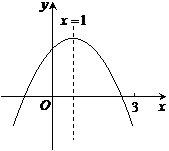
(第10题图)
[答案]D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com