
三、解答题:
21.解:在△ABC中,由正弦定理,
得sin B=sin A=×=;
又A=30°,且a<b,
∴B=60°或B=120°.
①当B=60°时,C=90°,△ABC为直角三角形,
故S△ABC=ab=6.
②当B=120°时,C=30°,△ABC为等腰三角形,
故S△ABC=absin C=×2×6sin30°=3.
17. 7 18.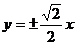 19.
19. 20.
20.
二、填空题:
13.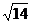 14.
14.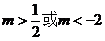 15.
5 16.
7
15.
5 16.
7
25.在数列 中,
中,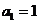 ,
,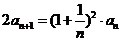 。
。
(Ⅰ)证明数列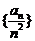 是等比数列,并求
是等比数列,并求 的通项公式;(Ⅱ)令
的通项公式;(Ⅱ)令 ,求数列
,求数列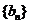 的前
的前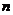 项和
项和 ;(Ⅲ)求数列
;(Ⅲ)求数列 的前
的前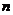 项和
项和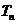 。
。
和风中学2013-2014学年第一学期高二(理)数期末综合复习
24. 如图,四边形
如图,四边形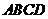 是边长为1的正方形,
是边长为1的正方形, 平面
平面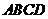 ,
,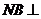 平面
平面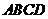 ,且
,且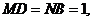
(1)求证: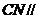 平面
平面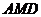 ;
;
(2)求面AMN与面NBC所成二面角的平面角的余弦值.
23.已知点A(-2,0),B(2,0),直线AP与直线AB相交于点P,它们的斜率之积为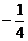 ,求点P的轨迹方程(化为标准方程).
,求点P的轨迹方程(化为标准方程).
22.设:P: 指数函数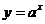 在x∈R内单调递减;Q:曲线
在x∈R内单调递减;Q:曲线 与x轴交于不同的两点。如果P为真,Q为假,求a的取值范围.
与x轴交于不同的两点。如果P为真,Q为假,求a的取值范围.
三、解答题
21.在△ABC中,已知a=2,b=6,A=30°,求B及S△ABC。
20.数列1,1+2,1+2+22,…,1+2+22+…+2n-1,…的前n项和为______________。
19.正方体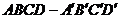 中,点
中,点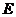 为
为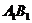 的中点,
的中点,
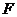 为
为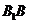 的中点,则
的中点,则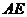 与
与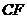 所成角的余弦值为
。
所成角的余弦值为
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com