2．（本题10分）四边形一条对角线所在直线上的点，如果到这条对角线的两端点的距离不相等，但到另一对角线的两个端点的距离相等，则称这点为这个四边形的准等距点．如图l，点P为四边形ABCD对角线AC所在直线上的一点，PB=PD，PA≠PC，则点P为四边形ABCD的准等距点．

（1）如图2，画出菱形ABCD的一个准等距点．

（2）如图3，作出四边形ABCD的一个准等距点(尺规作图，保留作图痕迹，不要求写作法)．

（3）如图4，在四边形ABCD中，P是AC上的点，PA≠PC，延长BP交CD于点E，延长DP交BC于点F，且∠CDF=∠CBE，CE=CF．试说明点P是四边形ABCD的准等距点．

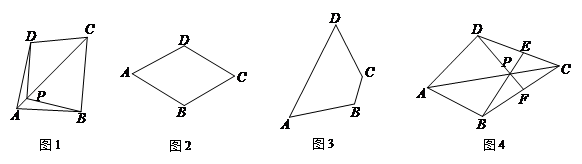
1．（本题10分）如图，在等腰梯形ABCD中，AB∥DC，AD=BC=5cm，AB=12cm，CD=6cm，点Q从C开始沿CD边向D移动，速度是每秒1厘米，点P从A开始沿AB向B移动，点P速度是每秒3厘米，如果点P，Q分别从A，C同时出发，当其中一点到达终点时运动停止．设运动时间为t秒．

（1）若四边形APQD是平行四边形时，求t的值；

（2）线段PQ是否可能平分对角线BD？若能，求t的值，若不能，请说明理由；

（3）若在某一时刻点P恰好在DQ的垂直平分线上，求此时t的值．

25．（本题7分）某蔬菜加工厂承担出口蔬菜加工任务，有一批蔬菜产品需要装入某一规格的纸箱．供应这种纸箱有两种方案可供选择：

方案一：从纸箱厂定制购买，每个纸箱价格为4元；

方案二：由蔬菜加工厂租赁机器自己加工制作这种纸箱，机器租赁费按生产纸箱数收取．工厂需要一次性投入机器安装等费用16000元，每加工一个纸箱还需成本费2.4元．

（1）若需要这种规格的纸箱个，请分别写出从纸箱厂购买纸箱的费用（元）和蔬菜加工厂自己加工制作纸箱的费用（元）关于（个）的函数关系式；

（2）假设你是决策者，你认为应该选择哪种方案？并说明理由．

附加题（计20分）：

24．（本题7分）如图，△ABC中，AB=AC，AD、AE分别是∠BAC和∠BAC外角的平分线，BE⊥AE．

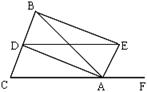（1）试说明：DA⊥AE；

（2）试判断AB与DE是否相等？并说明你的理由．

23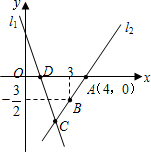．（本题7分）如图，直线l₁的函数关系式为y=－3x+3，且l₁与x轴交于点D，直线l₂经过点A、B，直线l₁、l₂交于点C.

（1）求点D 的坐标；

（2）求直线l₂的函数关系式；

（3）求△ADC的面积．

22．（本题7分）在一次消防演习中，消防员架起一架25米长的云梯，

如图（AB位置）斜靠在一面墙上，梯子底端B离墙(AO)的距离是7米。

（1）求这个梯子的顶端距地面有多高？

（2）、如果消防员接到命令，要求梯子的顶端下降4米

（梯子在CD位置 ，云梯长度不变），那么云梯的底部在

　水平方向应滑动多少米？

21．（本题6分）甲、乙两人在相同条件下各射靶10次，每次射靶的成绩情况如左图所示：

（1）请填写右表；

（2）请从平均数、中位数、9环（含9环）以上的次数以及折线的走势对测试结果进行综合分析，谁的成绩更好些？

三、解答题

　 19．（本题8分）

（1）计算：；

（2）解不等式组．

20. （本题6分）在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A，C的坐标分别为（—4，5），（—1，3）．

⑴请在如图所示的网格平面内作出平面直角坐标系；

⑵请作出△ABC关于y轴对称的△A′B′C′；

⑶写出点B′的坐标．

18．如图，有种动画程序，屏幕上正方形区域ABCD表示黑色物体甲．已知A (1，1)，B (2，1)，C (2，2)，D (1，2)，用信号枪沿直线y = 2x + b发射信号，当信号遇到区域甲（正方形ABCD包括边）时，甲由黑变白．则b的取值范围为　 ▲　 时，甲能由黑变白．

17．如图，已知函数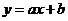和的图象交于点P，则二元一次方程组的解是　▲　 ．