2．下列命题中，真命题的是[　　 ]

　 A．相等的两个角是对顶角　　　　　　　　　　 B．若a>b，则>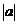

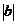
　 C．两条直线被第三条直线所截，内错角相等　　 D．等腰三角形的两个底角相等

一、选择题：

1．任意画一个三角形，它的三个内角之和为[　　 ]

　 A． 180°　　 　　　 B．270°　　 　　　 C．360°　　 　　　 D．720°

28、（本题满分12分）如图，在三角形ABC中，AB=6，AC=8，BC=10，点D、E分别是边AC、AB上的动点，以DE为直径作⊙O。

（1）如图1，如果DE为△ABC的中位线，试判断BC与⊙O的位置关系，并说明理由；

（2）在BC与⊙O相切的条件下：

①如图2，如果点A与点E重合，试求⊙O的半径；

②如图3，如果DE∥BC，试求⊙O的半径；

③求⊙O的半径的最小值（直接写出答案）。

盐城市中兴实验学校2013-2014学年度第一学期学情检测

27、（本题满分12分）

（1）如图1，在正方形ABCD中，M是BC边（不含端点B、C）上任意一点，P是BC延长线上一点，N是

∠DCP的平分线上一点．若∠AMN=90°，求证：AM=MN．

下面给出一种证明的思路，你可以按这一思路证明，也可以选择另外的方法证明．

证明：在边AB上截取AE=MC，连ME．正方形ABCD中，∠B=∠BCD=90°，AB=BC．

∴∠NMC=180°—∠AMN­—∠AMB=180°—∠B—∠AMB=∠MAB=∠MAE．

（下面请你完成余下的证明过程）

（2）若将（1）中的“正方形ABCD”改为“正三角形ABC”（如图2），N是∠ACP的平分线上一点，则当

∠AMN=60°时，结论AM=MN是否还成立？请说明理由．

（3）若将（1）中的“正方形ABCD”改为“正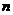边形ABCD……X”，请你作出猜想：当∠AMN=　　　 °时，结论AM=MN仍然成立．（直接写出答案，不需要证明）

26．（本题满分10分）某商店经销一批小家电，每个小家电的成本为40元。据市场分析，销售单价定为50元时，一个月能售出500件；若销售单价每涨1元，月销售量就减少10件．针对这种小家电的销售情况，请回答以下问题：

（1）填空：当销售单价定为60元时，月销售量为　　　　 ，月销售利润为　　　　 ；

（2）设销售单价定为x元（x>50），月销售利润为y元，求y与x的函数关系式(用含x的代数式表示)；

（3）现该商店要保证每月盈利8750元，同时又要使顾客得到实惠，那么销售单价应定为多少元？

25．（本题满分10分）如图，在单位长度为1的正方形网格中，一段圆弧经过格点A、B、C．（1）请完成如下操作：①以点O为原点、竖直和水平方向所在的直线为坐标轴、网格边长为单位长，建立平面直角坐标系；②画出该圆弧所在圆的圆心D的位置（不用写作法，保留作图痕迹），并连接AD、CD．

（2）请在（1）的基础上，完成下列问题：

①写出点的坐标：C _________（6，2）、D ________；（2，0）

②⊙D的半径为　　　　　　 　2 5

（结果保留根号）；

③若E（7，0），试判断直线EC与⊙D的位置关系并说明你的理由．

24．（本题满分8分）如图，AB是⊙O的切线，A为切点，AC是⊙O的弦，过0作于OH⊥AC于点H．

若OH=3，AB=12，BO=13．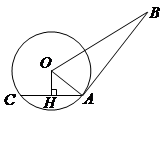

求：（1）⊙O的半径； （2）AC的值．

23．（本题满分8分）省射击队为了从甲、乙两名运动员中选拔一人参加全国比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：

（1）根据表格中的数据，计算出甲的平均成绩是　　　 环，乙的平均成绩是　　　 环；

（2）分别计算甲、乙两名运动员六次测试成绩的方差；　　　　　　　　　

（3）假如你是教练员，你认为推荐谁参加全国比赛更合适，请说明理由．

22．（本题满分8分）已知抛物线y＝ax²(a≠0)与直线y＝ 2x－3相交于点A(1，b)．求：

(1)a、b的值．　　　　 (2)另一个交点B的坐标．

21．（本题满分8分）如图，在△ABC中，D是BC边的中点，E、F分别在AD及其延长线上，

　CE∥BF，连接BE、CF．　

　(1)求证：△BDF≌△CDE；　 (2)若AB=AC，求证：四边形BFCE是菱形．