2．下面四个图形中，∠1=∠2一定成立的是（　　 ）．

一、选择题．

1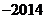．的相反数是（　　 ）．

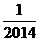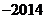　A．　　　 B．　　　 C．　　　　 D．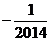　

25. （本小题满分14分）

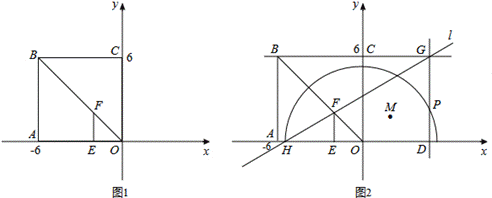
如图1，在平面直角坐标系中，正方形OABC的顶点A（－6，0），过点

E（－2，0）作EF∥AB，交BO于F；

（1）求EF的长；

（2）过点F作直线l分别与直线AO、直线BC交于点H、G；

①根据上述语句，在图1上画出图形，并证明；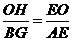

②过点G作直线GD∥AB，交x轴于点D，以圆O为圆心，OH长为半径在x轴上方作半圆（包括直径两端点），使它与GD有公共点P．如图2所示，当直线l绕点F旋转时，点P也随之运动，证明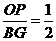：，并通过操作、观察，直接写出BG长度的取值范围（不必说理）；

（3）在（2）中，若点M（2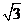，），探索2PO+PM的最小值．

24、（本小题满分14分）

如图，在平面直角坐标系中，抛物线与x轴交于A、B两点（A在B的左侧），与y轴交于点C（0，4），顶点为（1，）．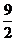

（1）求抛物线的函数关系式；

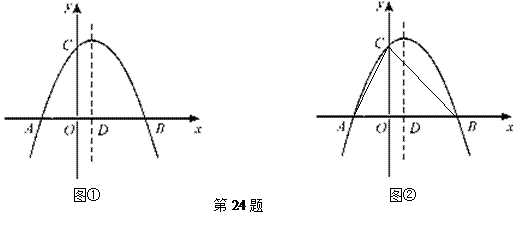
（2）如图①，设该抛物线的对称轴与x轴交于点D，试在对称轴上找出点P，使△CDP为等腰三角形，请直接写出满足条件的所有点P的坐标；

（3）如图②，连结AC、BC，若点E是线段AB上的一个动点（与点A、B不重合），过点E作EF∥AC交线段BC于点F，连结CE，记△CEF的面积为S，求出S的最大值及此时E点的坐标.

24、（本小题满分14分）

如图，在平面直角坐标系中，抛物线与x轴交于A、B两点（A在B

的左侧），与y轴交于点C（0，4），顶点为（1，）．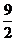

（1）求抛物线的函数关系式；

（2）如图①，设该抛物线的对称轴与x轴交于点D，试在对称轴上找出点P，使△CDP为等腰三角形，请直接写出满足条件的所有点P的坐标；

23、（本小题满分12分）

在锐角△ABC中，AB=4，BC=5，∠ACB=45°，将△ABC绕点B按逆时针方向旋转，得到△A₁BC₁．

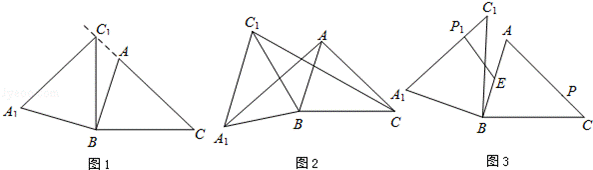
（1）如图1，当点C₁在线段CA的延长线上时，求∠CC₁A₁的度数；

（2）如图2，连接AA₁，CC₁．若△ABA₁的面积为4，求△CBC₁的面积；

（3）如图3，点E为线段AB中点，点P是线段AC上的动点，在△ABC绕点B按逆时针方向旋转过程中，点P的对应点是点P₁，求线段EP₁长度的最大值与最小值．

22、（本小题满分12分）

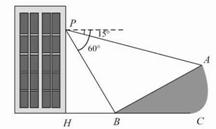如图，小明在大楼30米高（即PH=30米，且PH⊥HC）的窗口P处进行观测，测得山坡上A处的俯角为15°，山脚B处得俯角为60°，已知该山坡的坡度i（即tan∠ABC）为1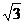：.（点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上）

（1）山坡坡角（即∠ABC）的度数等于________度；(直接填空)

（2）求A、B两点间的距离（结果精确到0.1米）

20、（本小题满分10分）

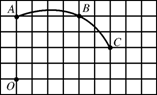
如图，在单位长度为1的正方形网格中，一段圆弧经过网格的交点A，B，C.

(1)请完成如下操作：

①以点O为原点、竖直和水平方向所在的直线为坐标轴、网格边长为单位长，建立平面直角坐标系；②用直尺和圆规画出该圆弧所在圆的圆心D的位置(不用写作法，保留作图痕迹)，并连接AD，CD；

(2)请在(1)的基础上，完成下列问题：

①写出点的坐标：C__________，D__________；

②⊙D的半径＝____________(结果保留根号)；

③若扇形ADC是一个圆锥的侧面展开图，则该圆锥的底面面积为________(结果保留π)；

④若点E(7,0)，试判断直线EC与⊙D的位置关系，并说明你的理由．

19、（本小题满分10分）

先化简，再求值：（x﹣1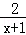）÷（﹣1），其中x为方程x²+3x+2=0的根．