
3.( ) He ________a worker in a factory, but he________ a pop star two years ago.
A. used to be; has become B. used to be; became
C. was used to be; becomes D. was used to being; has become
( )4—Ann is in hospital --- Oh, really? —I _____know. I ________her for a long time.
A. didn’t ; will see B.don’t ;will see
C. didn’t ; haven’t seen D.don’t ; haven’t seen
一、单项选择
( )1 great fun it is to surf the Internet!
A. What
B.
What a
C. How a
D. Ho w
w
2.( ) The car was running at such a high speed that the driver couldn’t ____ it and it crashed into the tree
A. save B. control C. order D. print
23. (本小题满分12分)如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点M,连接OM,过点M作⊙O的切线交边BC于N.
(1)图中是否存在与△ODM相似的三角形,若存在,请找出并给于证明。
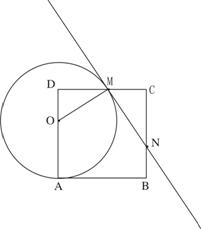 (2)设DM = x,OA=R,求R关于x 的函数关系式;是否存在整数R,使得利用正方形ABCD内部的扇形OAM围成的圆
(2)设DM = x,OA=R,求R关于x 的函数关系式;是否存在整数R,使得利用正方形ABCD内部的扇形OAM围成的圆 锥地面周长可以为4p ,若存在请求出此时DM的长;不存在,请说明理由。
锥地面周长可以为4p ,若存在请求出此时DM的长;不存在,请说明理由。
(3)在动点O逐渐向点D运动(OA 逐渐增大)的过程中,△CMN的周长如何变化?说明理由.
逐渐增大)的过程中,△CMN的周长如何变化?说明理由.

22.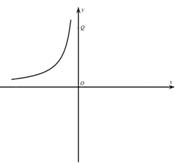 (本题12分)对于平面直角坐标系
xOy中的点P(a,b),若点
(本题12分)对于平面直角坐标系
xOy中的点P(a,b),若点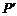 的坐标为(
的坐标为(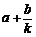 ,
,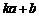 )(其中k为常数,且
)(其中k为常数,且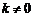 ),则称点
),则称点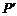 为点P的“k属派生点”.
为点P的“k属派生点”.
例如:P(1,4)的“2属派生点”为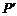 (1+
(1+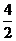 ,
,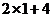 ),即
),即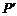 (3,6).
(3,6).
(1)求点P(-1,-2)的“2属派生点”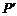 的坐标。
的坐标。
|
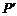 的坐标为(3,3),请写出两个符合条件的点P的坐标,你发
的坐标为(3,3),请写出两个符合条件的点P的坐标,你发 现了什么?
现了什么?
(3)若点P在x轴的正半轴上,点P的“k属派生点”为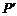 点,且△
点,且△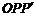 为等腰直角三角形,求k的值.
为等腰直角三角形,求k的值.
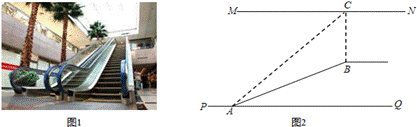
20.(本题8分)如图1,某超市从底楼到二楼有一自 动扶梯,图2是侧面示意图.已知自动扶梯AB的坡比为1:2.4,AB的长度是13米,MN是二楼楼顶,M
动扶梯,图2是侧面示意图.已知自动扶梯AB的坡比为1:2.4,AB的长度是13米,MN是二楼楼顶,M N
N ∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,求二楼的层高BC(精确到0.1米).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,求二楼的层高BC(精确到0.1米).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
19.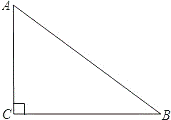 (本小题满分8分)
(本小题满分8分)
如图,已知△ABC中,∠ACB=90°。
(1)利用尺规作图,作一个点P,使得点P到∠ACB两边的距离相等,且PA=PB;
(2)试判断△ABP的形状,并说明理由。
18.(本小题满分8分)
当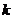 满足条件
满足条件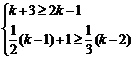 时,关于
时,关于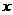 的一元二次方程
的一元二次方程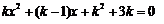 是否存在实数根
是否存在实数根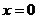 ,若存在求出
,若存在求出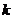 值,若不存在请说明理由.
值,若不存在请说明理由.
三、解答题
17. (本小题满分6分)
我们知道,代数式包括整式、分式以及根式。请你写出一个只含有字母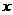 的二次三项式,并且不论当
的二次三项式,并且不论当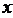 为何实数时,该代数式值恒为正数,并简要说明该代数式值恒为正数的理由。
为何实数时,该代数式值恒为正数,并简要说明该代数式值恒为正数的理由。
16.如图,抛物线y=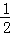 x2﹣
x2﹣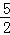 x与x轴交于O,A两点.半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动.两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动.设点P的横坐标为t.若⊙P与⊙Q相离,则t的取值范围是_____ ____ .
x与x轴交于O,A两点.半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动.两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动.设点P的横坐标为t.若⊙P与⊙Q相离,则t的取值范围是_____ ____ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com