
二、填空题:本大题共4个小题,每个小题5分。
(13)(x-2) 的展开式中
的展开式中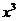 的系数为
.(用数字作答)
的系数为
.(用数字作答)
[答案]-160
(14)函数 的最大值为
.
的最大值为
.
[答案]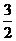
(15)设x,y满足约束条件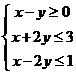 ,则z=x+4y的最大值为 .
,则z=x+4y的最大值为 .
[答案]5
(16)直线l1和l2是圆 的两条切线,若l1与l2的交点为(1,3),则l1与l2的交角的正切值
的两条切线,若l1与l2的交点为(1,3),则l1与l2的交角的正切值
等于 .
[答案]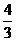
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)
设集合M={1,2,4,6,8},N={2,3,5,6,7},则M N中元素的格式为(
)
N中元素的格式为(
)
A. 2 B. 3 C. 5 D. 7
[答案]B
(2)已知角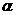 的终边经过点(-4,3),则cos
的终边经过点(-4,3),则cos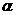 =( )
=( )
A. 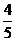 B.
B. 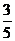 C.
-
C.
-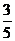 D. -
D. -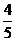
[答案]D
(3)不等式组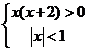 的解集为( )
的解集为( )
A. 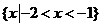 B.
B.  C.
C. 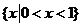 D.
D. 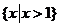
[答案]C
(4)已知正四面体ABCD中,E是AB的中点,则异面直线CE与BD所成角的余弦值为( )
A. 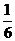 B.
B.
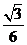 C.
C.
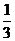 D.
D.
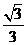
[答案]B
(5)函数y=ln(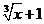 )(x>-1)的反函数是( )
)(x>-1)的反函数是( )
A. 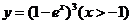 B.
B. 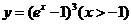
C. 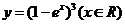 D.
D. 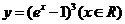 .
.
[答案]D
(6)已知a、b为单位向量,其夹角为60 ,则(2a-b)·b
=( )
,则(2a-b)·b
=( )
A. -1 B. 0 C. 1 D.2
[答案]B
(7)有6名男医生、5名女医生,从中选出2名男医生、1名女医生组成一个医疗小组,则不同的选法共有( )
A. 60种 B. 70种 C. 75种 D. 150种
[答案]C
(8)设等不数列{an}的前n项和为Sn,若S2=3,S4=15,则S6=( )
A. 31 B. 32 C. 63 D. 64
[答案]C
(9)已知椭圆C: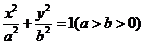 的左右焦点为F1,F2离心率为
的左右焦点为F1,F2离心率为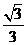 ,过F2的直线l交C与A,B两点,若△AF1B的周长为
,过F2的直线l交C与A,B两点,若△AF1B的周长为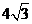 ,则C的方程为( )
,则C的方程为( )
A. 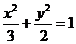 B.
B. 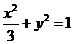 C.
C. 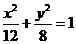 D.
D. 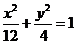
[答案]A
(10)正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积是( )
A. 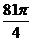 B.
16
B.
16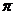 C. 9
C. 9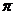 D.
D. 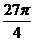
[答案]A
(11)双曲线C: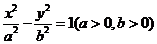 的离心率为2,焦点到渐近线的距离为
的离心率为2,焦点到渐近线的距离为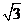 ,则C的焦距等于( )
,则C的焦距等于( )
A. 2
B. 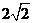 C.4
D.
C.4
D.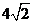
[答案]C
(12)奇函数f(x)的定义域为R,若f(x+2)为偶函数,则f(1)=1,则f(8)+f(9)= ( )
A. -2 B.-1 C. 0 D. 1
[答案]D
22.(本小题满分12分)
 某银行的一个营业窗口可办理四类业务,假设顾客办理业务所需的时间互相独立,且
某银行的一个营业窗口可办理四类业务,假设顾客办理业务所需的时间互相独立,且
都是整数分钟,经统计以往100位顾客办理业务所需的时间(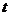 )结果如下:
)结果如下:
|
类别 |
A类 |
B类 |
C类 |
D类 |
|
顾客数(人) |
20 |
30 |
40 |
10 |
时间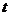 (分钟/人) (分钟/人) |
2 |
3 |
4 |
6 |

(注:银行工作人员在办理两项业务时的间隔时间忽略不计,并将频率视为概率.)
(Ⅰ)求银行工作人员恰好在第6分钟开始办理第三位顾客的业务的概率;
(Ⅱ)用 表示至第4分钟末已办理完业务的顾客人数,求
表示至第4分钟末已办理完业务的顾客人数,求 的分布列及数学期望.
的分布列及数学期望.
2013—2014学年上学期期中考试
21.(满分12分)经销商经销某种农产品,在一个销售季度内,每售出1 t该产品获利润500元,未售出的产品,每1 t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图6-3-14所示.经销商为下一个销售
季度购进了130 t该农产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.
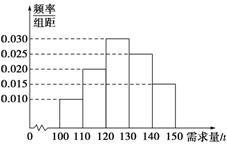
图6-3-14
(1)将T表示为X的函数;
(2)根据直方图估计利润T不少于57 000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若需求量X∈[100,110),则取X=105,且X=105的概率等于需求量落入[100,110)的频率).求T的数学期望.
20、(满分12分)松原市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于90分的有参赛资格,90分以下(不包括90分)的则被淘汰。若现有500人参加测试,学生成绩的频率分布直方图如下:
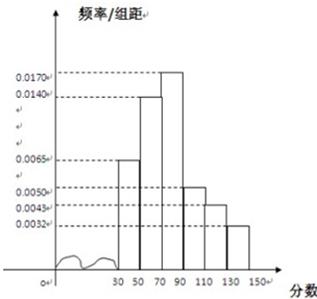 (I)求获得参赛资格的人数;(II)根据频率直方图,估算这500名学生测试的平均成绩;
(I)求获得参赛资格的人数;(II)根据频率直方图,估算这500名学生测试的平均成绩;
(III)若知识竞赛分初赛和复赛,在初赛中每人最多有5次选题答题的机会,累计答对3题或答错3题即终止,答对3题者方可参加复赛,已知参赛者甲答 对每一个问题的概率都相同,并且相互之间没有影响,已知他连续两次答错的概率为
对每一个问题的概率都相同,并且相互之间没有影响,已知他连续两次答错的概率为 ,
,
求甲在初赛中答题个数的分布列及数学期望.
19、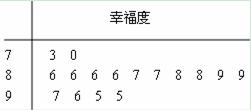 (满分12分)前不久,省社科院发布了2013年度“安徽城市居民幸福排行榜”,芜湖市成为本年度安徽最“幸福城”.随后,师大附中学生会组织部分同学,用“10分
(满分12分)前不久,省社科院发布了2013年度“安徽城市居民幸福排行榜”,芜湖市成为本年度安徽最“幸福城”.随后,师大附中学生会组织部分同学,用“10分 制”随机调查“阳光”社区人们的幸福度.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
制”随机调查“阳光”社区人们的幸福度.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
(Ⅰ)指出这组数据的众数和中位数;
(Ⅱ)若幸福度不低于9.5分,则称该人的幸福度为“极幸福”.求从这16人中随机选取3人,至多有1人是“极幸福”的概率;
(Ⅲ)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记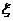 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求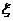 的分布列及数学期望.
的分布列及数学期望.
18、(本小题满分12分)
PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,根据现行国家标准GB3095 – 2012,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米 ~ 75毫克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标。
从某自然保护区2012年全年每天的PM2.5监测值数据中随机地抽取10天的数据作为样本,监测值频数如下表所示:
|
PM2.5日均值 (微克/立方米) |
[25,35] |
(35,45] |
(45,55] |
(55,65] |
(65,75] |
(75,85] |
|
频数 |
3 |
1 |
1 |
1 |
1 |
3 |
(1)从这10天的PM2.5日均值监测数据中,随机抽取3天,求恰有1天空气质量达到一级的概率;
(2)从这10天的数据中任取3天数据,记ξ表示抽到PM2.5监测数据超标的天数,求ξ的分布列;
(3)以这 10天的PM2.5日均值来估计一年的空气质量状况,则一年(按366天算)中平均有多少天的空气质
10天的PM2.5日均值来估计一年的空气质量状况,则一年(按366天算)中平均有多少天的空气质 量达到一级或二级。(精确到整数)
量达到一级或二级。(精确到整数)
三、简答题
17.(10分) 户外运动已经成为一种时尚运动,某单位为了了解员工喜欢户外运动是否与性别有关,决定从本单位全体650人中采用分层抽样的办法抽取50人进行问卷调查,得到了如下列联表:
|
|
喜欢户外运动 |
不喜欢户外运动 |
合计 |
|
男性 |
|
5 |
|
|
女性 |
10 |
|
|
|
合计 |
|
|
50 |
已知在这50人中随机抽取1人抽到喜欢户外运动的员工的概率是.
(1)请将上面的列联表补充完整;(2)求该公司男、女员工各多少名;
(3)是否有99.5%的把握认为喜欢户外运动与性别有关?并说明你的理由.
下面的临界值表仅供参考:
|
P(K2≥k) |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
k |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
参考公式:K2=,其中n=a+b+c+d
16.随机变量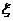 的分布列如下图:其中
的分布列如下图:其中 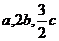 成等差数列,若
成等差数列,若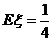 ,则
,则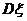 的值是 .
的值是 .
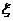
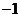
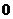

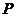

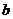

15.某种产品的广告费支出x与销售额y之间有如下对应数据(单位:百万元).
|
x |
2 |
4 |
5 |
6 |
8 |
|
y |
30 |
40 |
60 |
t |
70 |
根据上表提供的数据,求出y关于x的线性回归方程为=6.5x+17.5,则表中t的值为________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com