
21. (本小题满分12分)
已知函数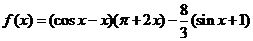 ,
,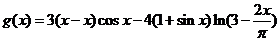 .
.
证明:(1)存在唯一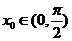 ,使
,使 ;
;
(2)存在唯一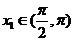 ,使
,使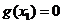 ,且对(1)中的
,且对(1)中的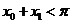 .
.
请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分,作答时用2B铅笔在答题卡上把所选题目对应题号下方的方框涂黑.
20. (本小题满分12分)
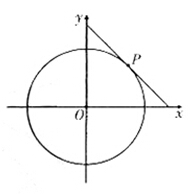
圆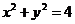 的切线与x轴正半轴,y轴正半轴围成一个三角形,当该三角形面积最小时,切点为P(如图),双曲线
的切线与x轴正半轴,y轴正半轴围成一个三角形,当该三角形面积最小时,切点为P(如图),双曲线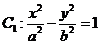 过点P且离心率为
过点P且离心率为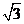 .
.
(1)求 的方程;
的方程;
(2)椭圆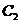 过点P且与
过点P且与 有相同的焦点,直线
有相同的焦点,直线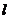 过
过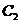 的右焦点且与
的右焦点且与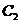 交于A,B两点,若以线段AB为直径的圆心过点P,求
交于A,B两点,若以线段AB为直径的圆心过点P,求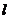 的方程.
的方程.
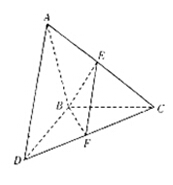
19. (本小题满分12分)
如图, 和
和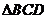 所在平面互相垂直,且
所在平面互相垂直,且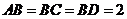 ,
,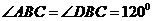 ,E、F分别为AC、DC的中点.
,E、F分别为AC、DC的中点.
(1)求证: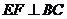 ;
;
(2)求二面角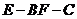 的正弦值.
的正弦值.
18. (本小题满分12分)
一家面包房根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,如图所示:
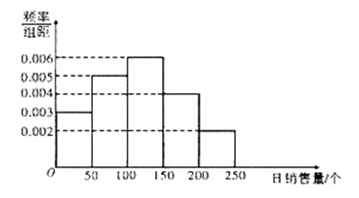
将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
(1)求在未来连续3天里,有连续2天的日销售量都不低于100个且另一天的日销售量低于50个的概率;
(2)用X表示在未来3天里日销售量不低于100个的天数,求随机变量X的分布列,期望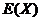 及方差
及方差 .
.
三、解答题
17.(本小题满分12分)
在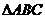 中,内角A,B,C的对边a,b,c,且
中,内角A,B,C的对边a,b,c,且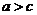 ,已知
,已知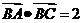 ,
,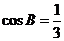 ,
,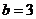 ,求:
,求:
(1)a和c的值;
(2) 的值.
的值.
16.对于 ,当非零实数a,b满足
,当非零实数a,b满足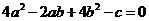 ,且使
,且使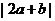 最大时,
最大时,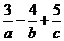 的最小值为
.
的最小值为
.
15.已知椭圆C: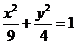 ,点M与C的焦点不重合,若M关于C的焦点的对称点分别为A,B,线段MN的中点在C上,则
,点M与C的焦点不重合,若M关于C的焦点的对称点分别为A,B,线段MN的中点在C上,则 . ZXXK
. ZXXK
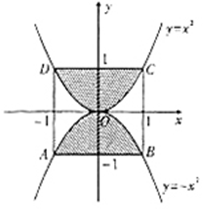
14.正方形的四个顶点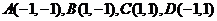 分别在抛物线
分别在抛物线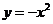 和
和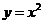 上,如图所示,若将一个质点随机投入正方形ABCD中,则质点落在阴影区域的概率是
.
上,如图所示,若将一个质点随机投入正方形ABCD中,则质点落在阴影区域的概率是
.
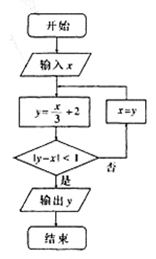
二、填空题
13.执行右侧的程序框图,若输入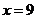 ,则输出
,则输出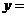 . ZXXK
. ZXXK
12.已知定义在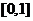 上的函数
上的函数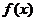 满足:
满足:
① ;
;
②对所有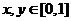 ,且
,且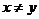 ,有
,有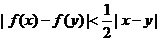 .
.
若对所有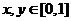 ,
,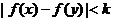 ,则k的最小值为( )
,则k的最小值为( )
A. B.
B.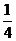 C.
C.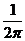 D.
D.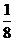
第Ⅱ卷(共90分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com