
三、解答题:
(17)(本小题满分12分)
四边形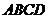 的内角
的内角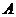 与
与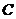 互补,
互补,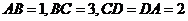 .
.
(1)求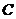 和
和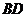 ;
;
(2)求四边形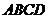 的面积.
的面积.
(18)(本小题满分12分)
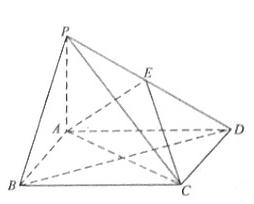
如图,四棱锥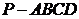 中,底面
中,底面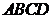 为矩形,
为矩形,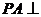 平面
平面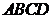 ,
,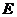 是
是 的重点.
的重点.
(1)证明: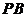 //平面
//平面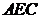 ;
;
(2)设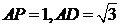 ,三棱锥
,三棱锥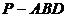 的体积
的体积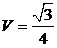 ,求
,求 到平面
到平面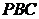 的距离.
的距离.
(19)(本小题满分12分)
某市为了考核甲、乙两部门的工作情况,随机访问了50位市民,根据这50位市民对这两部门的评分(评分越高表明市民的评价越高),绘制茎叶图如下:
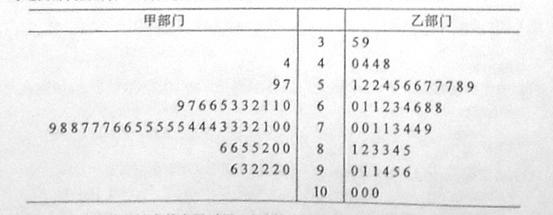
(1)分别估计该市的市民对甲、乙两部门评分的中位数;
(2)分别估计该市的市民对甲、乙两部门的评分高于90的概率;
(3)根据茎叶图分析该市的市民对甲、乙两部门的评价.
(20)(本小题满分12分)
设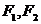 分别是椭圆C:
分别是椭圆C: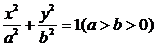 的左右焦点,
的左右焦点,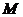 是
是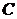 上一点且
上一点且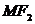 与
与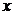 轴垂直,直线
轴垂直,直线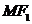 与
与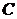 的另一个交点为
的另一个交点为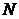 .
.
(1)若直线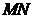 的斜率为
的斜率为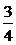 ,求
,求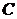 的离心率;
的离心率;
(2)若直线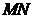 在
在 轴上的截距为
轴上的截距为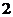 ,且
,且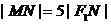 ,求
,求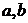 .
.
(21)(本小题满分12分)
已知函数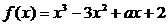 ,曲线
,曲线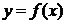 在点
在点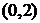 处的切线与
处的切线与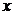 轴交点的横坐标为
轴交点的横坐标为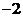 .
.
(1)求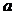 ;
;
(2)证明:当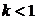 时,曲线
时,曲线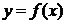 与直线
与直线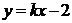 只有一个交点.
只有一个交点.
请考生在第22,23,24题中任选一题做答,如多做,则按所做的第一题记分。
(22)(本小题满分10分)选修4-1:几何证明选讲
如图,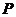 是
是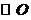 外一点,
外一点,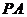 是切线,
是切线, 为切点,割线
为切点,割线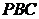 与
与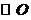 相交于
相交于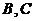 ,
,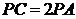 ,
,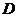 为
为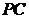 的中点,
的中点,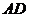 的延长线交
的延长线交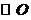 于点
于点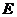 .证明:
.证明:
(1)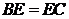 ;
;
(2)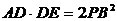
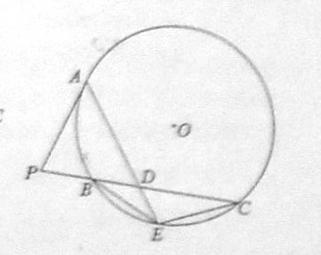
(23)(本小题满分10分)选修4-4:坐标系与参数方程
在直角坐标系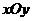 中,以坐标原点为极点,
中,以坐标原点为极点,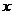 轴正半轴为极轴建立极坐标系,半圆
轴正半轴为极轴建立极坐标系,半圆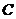 的极坐标方程为
的极坐标方程为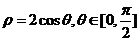 .
.
(1)求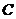 得参数方程;
得参数方程;
(2)设点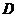 在
在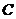 上,
上,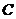 在
在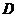 处的切线与直线
处的切线与直线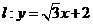 垂直,根据(1)中你得到的参数方程,确定
垂直,根据(1)中你得到的参数方程,确定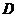 的坐标.
的坐标.
(24)(本小题满分10分)选修4-5:不等式选讲
设函数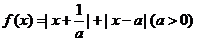
(1)证明: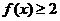 ;
;
(2)若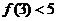 ,求
,求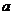 的取值范围.
的取值范围.
2014年普通高等学校招生全国统一考试
二、填空题:本大题共4小题,每小题5分.
(13)甲,乙两名运动员各自等可能地从红、白、蓝3种颜色的运动服中选择1种,则他们选择相同颜色运动服的概率为_______.
(14) 函数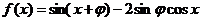 的最大值为________.
的最大值为________.
(15) 偶函数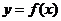 的图像关于直线
的图像关于直线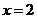 对称,
对称,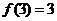 ,则
,则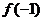 =________.
=________.
(16) 数列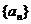 满足
满足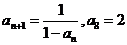 ,则
,则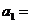 ________.
________.
一.选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)已知集合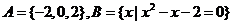 ,则
,则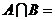 ( )
( )
A. 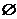 B.
B.
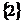 C.
C.
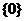 D.
D.
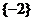
(2)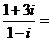 ( )
( )
A.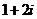 B.
B. 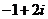 C.
C. 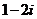 D.
D. 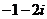
(3)函数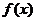 在
在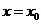 处导数存在,若
处导数存在,若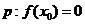 :
: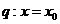 是
是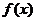 的极值点,则
的极值点,则
A.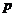 是
是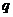 的充分必要条件
的充分必要条件
B. 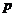 是
是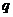 的充分条件,但不是
的充分条件,但不是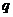 的必要条件
的必要条件
C. 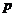 是
是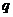 的必要条件,但不是
的必要条件,但不是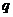 的充分条件
的充分条件
D. 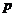 既不是
既不是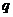 的充分条件,也不是
的充分条件,也不是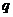 的必要条件
的必要条件
(4)设向量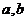 满足
满足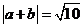 ,
,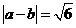 ,则
,则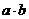 =( )
=( )
A. 1 B. 2 C. 3 D. 5
(5)等差数列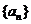 的公差是2,若
的公差是2,若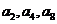 成等比数列,则
成等比数列,则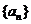 的前
的前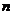 项和
项和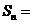 ( )
( )
A. 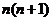 B.
B.
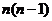 C.
C. 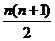 D.
D.
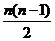
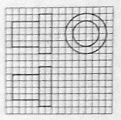
(6)如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6cm的圆柱体毛坯切削得到,则切削的部分的体积与原来毛坯体积的比值为( )
A.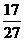 B.
B.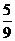 C.
C.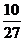 D.
D.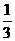
(7)正三棱柱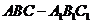 的底面边长为
的底面边长为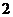 ,侧棱长为
,侧棱长为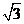 ,
,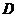 为
为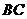 中点,则三棱锥
中点,则三棱锥
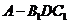 的体积为
的体积为
(A)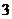 (B)
(B)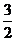 (C)
(C)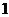 (D)
(D)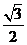
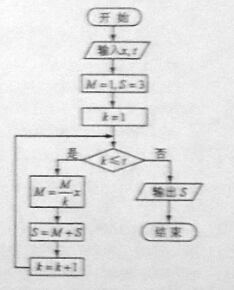
(8)执行右面的程序框图,如果输入的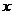 ,
,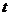 均为
均为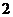 ,则输出的
,则输出的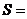
(A)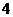 (B)
(B)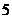 (C)
(C)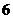 (D)
(D)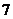
(9)设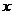 ,
,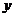 满足约束条件
满足约束条件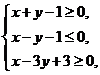 则
则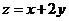 的最大值为
的最大值为
(A)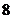 (B)
(B)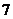 (C)
(C)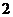 (D)
(D)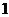
(10)设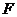 为抛物线
为抛物线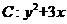 的焦点,过
的焦点,过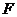 且倾斜角为
且倾斜角为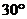 的直线交
的直线交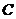 于
于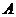 ,
,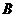 两点,则
两点,则
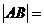
(A)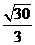 (B)
(B)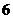 (C)
(C)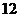 (D)
(D)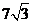
(11)若函数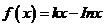 在区间
在区间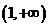 单调递增,则
单调递增,则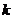 的取值范围是
的取值范围是
(A)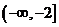 (B)
(B)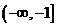 (C)
(C)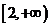 (D)
(D)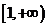
(12)设点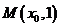 ,若在圆
,若在圆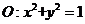 上存在点
上存在点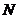 ,使得
,使得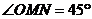 ,则
,则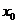 的取
的取
值范围是
(A)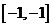 (B)
(B)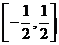 (C)
(C)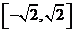 (D)
(D)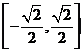
24. (本小题满分10分)选修4—5:不等式选讲
若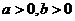 ,且
,且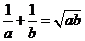 .
.
(Ⅰ) 求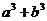 的最小值;
的最小值;
(Ⅱ)是否存在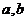 ,使得
,使得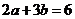 ?并说明理由.
?并说明理由.
23. (本小题满分10分)选修4—4:坐标系与参数方程
已知曲线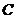 :
: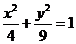 ,直线
,直线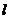 :
: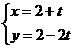 (
(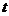 为参数).
为参数).
(Ⅰ)写出曲线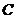 的参数方程,直线
的参数方程,直线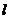 的普通方程;
的普通方程;
(Ⅱ)过曲线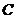 上任一点
上任一点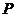 作与
作与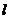 夹角为
夹角为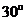 的直线,交
的直线,交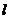 于点
于点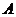 ,求
,求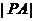 的最大值与最小值.
的最大值与最小值.
22. (本小题满分10分)选修4—1:几何证明选讲
(本小题满分10分)选修4—1:几何证明选讲
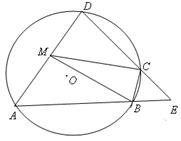
如图,四边形ABCD是⊙O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE
.(Ⅰ)证明:∠D=∠E;
(Ⅱ)设AD不是⊙O的直径,AD的中点为M,且MB=MC,证明:△ADE为等边三角形.
21. (本小题满分12分)设函数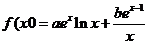 ,曲线
,曲线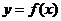 在点(1,
在点(1,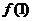 处的切线为
处的切线为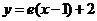 . (Ⅰ)求
. (Ⅰ)求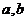 ; (Ⅱ)证明:
; (Ⅱ)证明: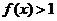 .
.
请考生从第(22)、(23)、(24)三题中任选一题作答。注意:只能做所选定的题目。如果多做,则按所做的第一个题目计分,作答时请用2B铅笔在答题卡上将所选题号后的 方框涂黑。
20. (本小题满分12分) 已知点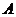 (0,-2),椭圆
(0,-2),椭圆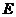 :
: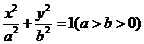 的离心率为
的离心率为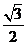 ,
,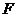 是椭圆的焦点,直线
是椭圆的焦点,直线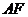 的斜率为
的斜率为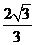 ,
,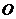 为坐标原点.
为坐标原点.
(Ⅰ)求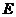 的方程;
的方程;
(Ⅱ)设过点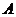 的直线
的直线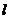 与
与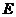 相交于
相交于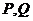 两点,当
两点,当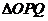 的面积最大时,求
的面积最大时,求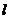 的方程.
的方程.
19.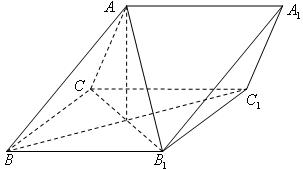 (本小题满分12分)如图三棱锥
(本小题满分12分)如图三棱锥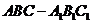 中,侧面
中,侧面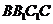 为菱形,
为菱形,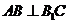 .
.
(Ⅰ) 证明: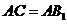 ;
;
(Ⅱ)若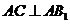 ,
,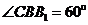 ,AB=Bc,求二面角
,AB=Bc,求二面角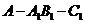 的余弦值.
的余弦值.
18. (本小题满分12分)从某企业的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:
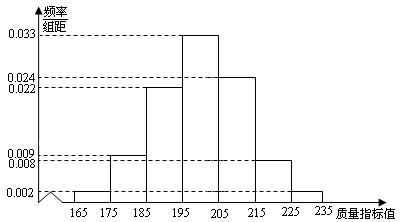
(Ⅰ)求这500件产品质量指标值的样本平均数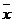 和样本方差
和样本方差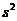 (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);
(Ⅱ)由频率分布直方图可以认为,这种产品的质量指标值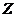 服从正态分布
服从正态分布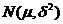 ,其中
,其中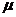 近似为样本平均数
近似为样本平均数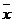 ,
,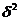 近似为样本方差
近似为样本方差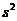 .
.
(i)利用该正态分布,求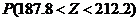 ;
;
(ii)某用户从该企业购买了100件这种产品,记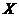 表示这100件产品中质量指标值为于区间(187.8,212.2)的产品件数,利用(i)的结果,求
表示这100件产品中质量指标值为于区间(187.8,212.2)的产品件数,利用(i)的结果,求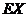 .
.
附: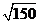 ≈12.2.
≈12.2.
若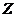 ~
~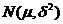 ,则
,则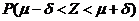 =0.6826,
=0.6826, =0.9544.
=0.9544.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com