
3.若变量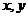 满足约束条件
满足约束条件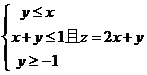 的最大值和最小值分别为
的最大值和最小值分别为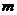 和
和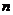 ,则
,则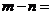
A.5 B.6 C.7 D.8
2.已知复数Z满足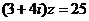 ,则Z=
,则Z=
A. 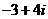 B.
B. 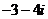 C.
C. 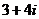 D.
D. 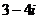
一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合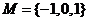 ,
,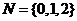 ,则
,则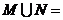
A. 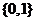 B.
B. 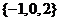 C.
C. 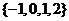 D.
D. 
21.(本小题满分13分)设实数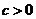 ,整数
,整数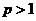 ,
,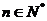 。
。
(I)证明:当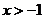 且
且 时,
时,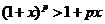 ;
;
(II)数列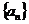 满足
满足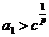 ,
,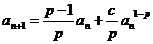 ,
,
证明: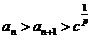 。
。
20.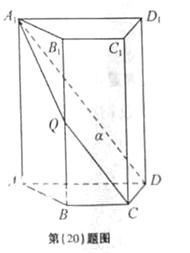 (本题满分13分)如图,四棱柱
(本题满分13分)如图,四棱柱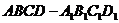 中,
中,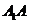
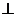 底面
底面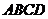 .四边形
.四边形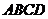 为梯形,
为梯形,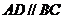 ,且
,且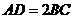 .过
.过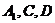 三点的平面记为
三点的平面记为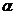 ,
,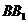 与
与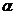 的交点为
的交点为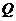 。(Ⅰ)证明:
。(Ⅰ)证明: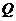 为
为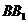 的中点;
的中点;
(Ⅱ)求此四棱柱被平面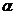 所分成上下两部分的体积之比;
所分成上下两部分的体积之比;
(Ⅲ)若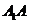
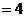 ,
,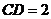 ,梯形
,梯形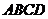 的面积为6,求
的面积为6,求
平面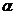 与底面
与底面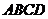 所成二面角大小。
所成二面角大小。
19.(本小题满分13分)如图,已知两条抛物线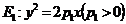 和
和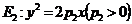 ,
,
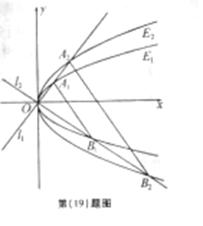 过原点
过原点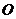 的两条直线
的两条直线 和
和 ,
, 与
与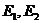 分别交于
分别交于 两点,
两点, 与
与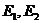 分别交于
分别交于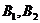 两点。
两点。
(Ⅰ)证明: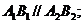
(Ⅱ)过原点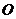 作直线
作直线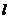 (异于
(异于 ,
, )与
)与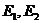 分别交于
分别交于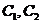 两点。
两点。
记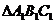 与
与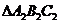 的面积分别为
的面积分别为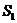 与
与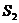 ,求
,求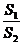 的值。
的值。
18.(本小题满分12分)设函数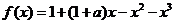 其中
其中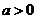 。
。
(Ⅰ)讨论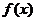 在其定义域上的单调性;
在其定义域上的单调性;
(Ⅱ)当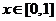 时,求
时,求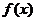 取得最大值和最小值时的
取得最大值和最小值时的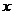 的值。
的值。
17.(本小题满分12分)甲乙两人进行围棋比赛,约定先连胜两局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛,假设每局甲获胜的概率为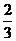 ,乙获胜的概率为
,乙获胜的概率为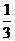 ,各局比赛结果相互独立。
,各局比赛结果相互独立。
(Ⅰ)求甲在4局以内(含4局)赢得比赛的概率;
(Ⅱ)记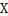 为比赛决出胜负时的总局数,求
为比赛决出胜负时的总局数,求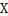 的分布列和均值(数学期望)。
的分布列和均值(数学期望)。
三.解答题:本大题共6小题,共75分。解答应写出文字说明、证明过程或演算步骤。解答写在答题卡上的指定区域内。
16.(本小题满分12分)设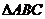 的内角
的内角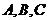 所对边的长分别是
所对边的长分别是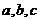 ,且
,且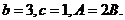
(Ⅰ)求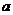 的值; (Ⅱ)求
的值; (Ⅱ)求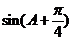 的值。
的值。
15.已知两个不相等的非零向量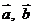 ,两组向量
,两组向量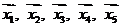 和
和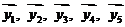 均由2个
均由2个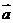 和3个
和3个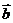 排列而成。记
排列而成。记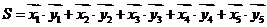 ,
,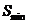 表示
表示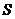 所有可能取值中的最小值。则下列命题的是_________(写出所有正确命题的编号)。
所有可能取值中的最小值。则下列命题的是_________(写出所有正确命题的编号)。
①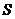 有5个不同的值。
有5个不同的值。
②若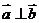 则
则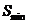 与
与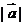 无关。
无关。
③若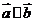 则
则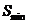 与
与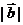 无关.
无关.
④若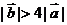 ,则
,则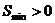 。
。
⑤若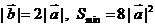 ,则
,则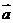 与
与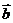 的夹角为
的夹角为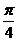
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com