
4. 若变量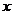 ,
,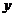 满足约束条件
满足约束条件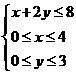 ,则
,则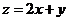 的最大值等于
的最大值等于
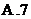
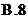
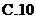
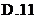
3. 已知向量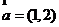 ,
,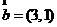 ,则
,则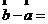
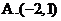
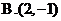
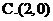
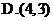
2. 已知复数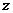 满足
满足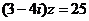 ,则
,则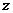
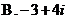

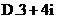
一、选择题:本大题共10小题,每小题5分,满分50分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合 ,
,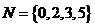 ,则
,则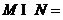
23.解:(1)由题得,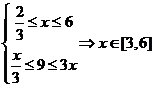
(理科)(2)由题得,∵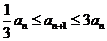 ,且数列
,且数列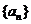 是等比数列,
是等比数列,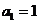 ,
,
∴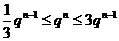 ,∴
,∴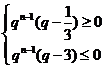 ,∴
,∴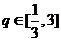 。
。
又∵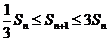 ,∴当
,∴当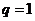 时,
时,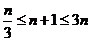 对
对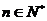 恒成立,满足题意。
恒成立,满足题意。
当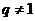 时,
时,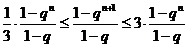
∴①当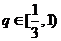 时,
时,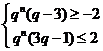 ,由单调性可得,
,由单调性可得,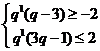 ,解得,
,解得,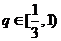
②当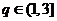 时,
时,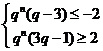 ,由单调性可得,
,由单调性可得,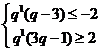 ,解得,
,解得,
(理科)(3)由题得,∵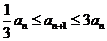 ,且数列
,且数列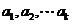 成等差数列,
成等差数列,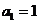 ,
,
∴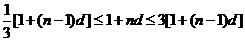 ,∴
,∴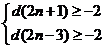 ,∴
,∴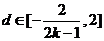
又∵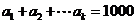 ,∴
,∴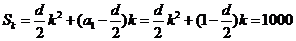
∴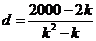 ,∴
,∴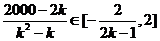 ,解得,
,解得,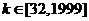 ,
,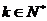
∴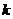 的最大值为1999,此时公差为
的最大值为1999,此时公差为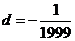
22.证明:(1)由题得,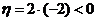 ,∴
,∴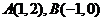 被直线
被直线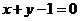 分隔。
分隔。
解:(2)由题得,直线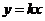 与曲线
与曲线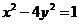 无交点
无交点
即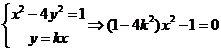 无解
无解
∴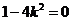 或
或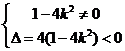 ,∴
,∴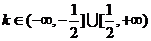
证明:(理科)(3)由题得,设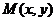 ,∴
,∴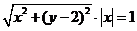 ,
,
化简得,点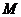 的轨迹方程为
的轨迹方程为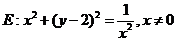 。
。
①当过原点的直线斜率存在时,设方程为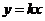 。
。
联立方程,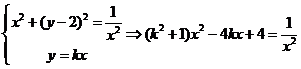 。
。
令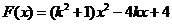 ,
,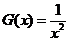 ,显然
,显然 是开口朝上的二次函数
是开口朝上的二次函数
∴由二次函数与幂函数的图像可得,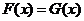 必定有解,不符合题意,舍去
必定有解,不符合题意,舍去
②当过原点的直线斜率不存在时,其方程为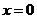 。
。
显然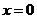 与曲线
与曲线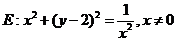 没有交点,在曲线
没有交点,在曲线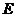 上找两点
上找两点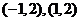 。
。
∴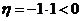 ,符合题意
,符合题意
综上所述,仅存在一条直线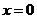 是
是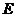 的分割线。
的分割线。
证明:(文科)(3)由题得,设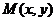 ,∴
,∴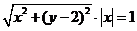 ,
,
化简得,点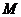 的轨迹方程为
的轨迹方程为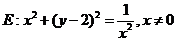 。
。
显然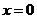 与曲线
与曲线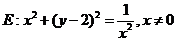 没有交点,在曲线
没有交点,在曲线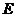 上找两点
上找两点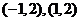 。
。
∴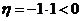 ,符合题意。∴
,符合题意。∴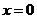 是
是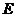 的分割线。
的分割线。
21.解:(1)由题得,∵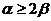 ,且
,且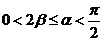 ,
,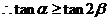
即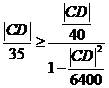 ,解得,
,解得, ,∴
,∴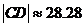 米
米
(2)由题得,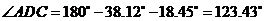 ,
,
∵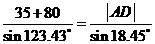 ,∴
,∴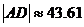 米
米
∵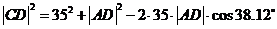 ,∴
,∴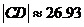 米
米
20.解:(1)由题得,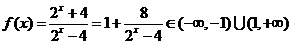
∴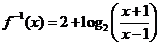 ,
,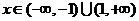
(2)∵ 且
且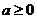
∴①当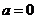 时,
时,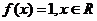 ,
,
∴对任意的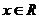 都有
都有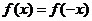 ,∴
,∴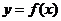 为偶函数
为偶函数
②当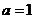 时,
时,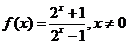 ,
, ,
,
∴对任意的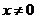 且
且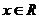 都有
都有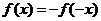 ,∴
,∴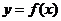 为奇函数
为奇函数
③当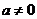 且
且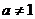 时,定义域为
时,定义域为 ,
,
∴定义域不关于原定对称,∴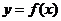 为非奇非偶函数
为非奇非偶函数
19.解:∵由题得,三棱锥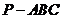 是正三棱锥
是正三棱锥
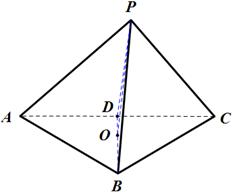
∴侧棱与底边所成角相同且底面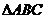 是边长为2的正三角形
是边长为2的正三角形
 ∴由题得,
∴由题得,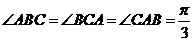 ,
,
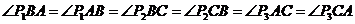
又∵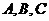 三点恰好在
三点恰好在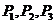 构成的
构成的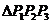 的三条边上
的三条边上
∴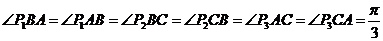
∴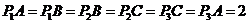
∴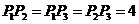 ,三棱锥
,三棱锥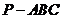 是边长为2的正四面体
是边长为2的正四面体
∴如右图所示作图,设顶点 在底面
在底面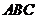 内的投影为
内的投影为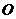 ,连接
,连接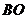 ,并延长交
,并延长交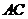 于
于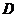
∴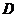 为
为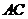 中点,
中点,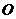 为
为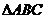 的重心,
的重心,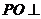 底面
底面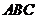
∴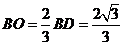 ,
, ,
,
23.(本题满分18分)本题共3个小题,第1小题满分3分,第2小题满分6分,第3小题满分9分.
已知数列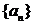 满足
满足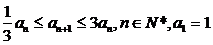 .
.
(1)若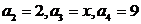 ,求
,求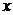 的取值范围;
的取值范围;
(2)若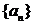 是公比为
是公比为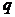 等比数列,
等比数列,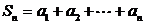 ,zxxk
,zxxk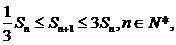 求
求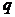 的取值范围;
的取值范围;
(3)若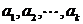 成等差数列,且
成等差数列,且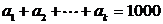 ,求正整数
,求正整数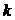 的最大值,以及
的最大值,以及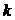 取最大值时相应数列
取最大值时相应数列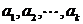 的公差.
的公差.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com