
7.在方程组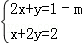 中,若未知数x,y满足x+y>0,则m的取值范围在数轴上的表示应是如图所示的( )
中,若未知数x,y满足x+y>0,则m的取值范围在数轴上的表示应是如图所示的( )
|
|
A. |
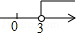 |
B. |
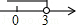 |
C. |
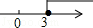 |
D. |
 |
6.不等式组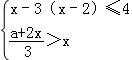 无解,则a的取值范围是( )
无解,则a的取值范围是( )
5.(4分)(2005•常州)将100个数据分成8个组,如下表:则第六组的频数为( )
|
组号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
频数 |
11 |
14 |
12 |
13 |
13 |
x |
12 |
10 |
|
|
A. |
12 |
B. |
13 |
C. |
14 |
D. |
15 |
4.已知不等式3x﹣a≤0的正整数解恰是1,2,3,4,那么a的取值范围是( )
|
|
A. |
a>12 |
B. |
12≤a≤15 |
C. |
12<a≤15 |
D. |
12≤a<15 |
|
2. 在1000个数据中,用适当的方法抽取50个体为样本进行统计,频数分布表中54.5~57.5这一组的频率为0.12,估计总体数据落在54.5~57.5之间的约有( )个.
|
|
A. |
120 |
B. |
60 |
C. |
12 |
D. |
6 |
3 设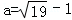 ,a在两个相邻整数之间,则这两个整数是( )
,a在两个相邻整数之间,则这两个整数是( )
|
|
A. |
1和2 |
B. |
2和3 |
C. |
3和4 |
D. |
4和5 |
一、选择题
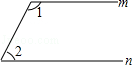
1.如图,若m∥n,∠1=105°,则∠2=( )
|
|
A. |
55° |
B. |
60° |
C. |
65° |
D. |
75° |
三、解答题
16
解: 由三角形面积公式,得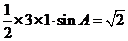 ,故
,故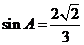
因为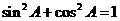 ,
,
所以
①当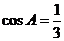 时,由余弦定理得
时,由余弦定理得
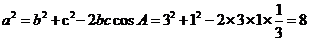 ,
,
所以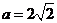
②当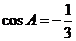 时,由余弦定理得
时,由余弦定理得
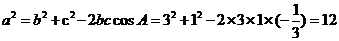 ,
,
所以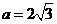
17
解: (Ⅰ)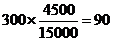 ,所以应收集90位女生的样本数据。
,所以应收集90位女生的样本数据。
(Ⅱ)由频率分布直方图得 ,所以该校学生每周平均体育运动时间超过4小时的概率的估计值为
,所以该校学生每周平均体育运动时间超过4小时的概率的估计值为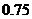 。
。
(Ⅲ)由(Ⅱ)知,300为学生中有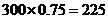 人的每周平均体育运动时间超过4小时,75人的每周平均体育运动时间不超过4小时,又因为样本数据中有210份是关于男生的,90份是关于女生的,所以每周平均运动时间与性别列联表如下:
人的每周平均体育运动时间超过4小时,75人的每周平均体育运动时间不超过4小时,又因为样本数据中有210份是关于男生的,90份是关于女生的,所以每周平均运动时间与性别列联表如下:
每周平均体育运动时间与性别列联表
|
|
男生 |
女生 |
总计 |
|
每周平均体育运动时间 不超过4小时 |
45 |
30 |
75 |
|
每周平均体育运动时间 超过4小时 |
165 |
60 |
225 |
|
总计 |
210 |
90 |
300 |
结合列联表可算得
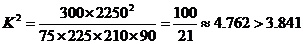
所以,有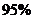 的把握认为“该校学生的每周平均体育运动时间与性别有关”。
的把握认为“该校学生的每周平均体育运动时间与性别有关”。
18
(Ⅰ)证:由已知可得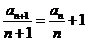 ,即
,即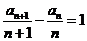
所以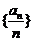 是以
是以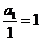 为首项,1为公差的等差数列。
为首项,1为公差的等差数列。
(Ⅱ)解:由(Ⅰ)得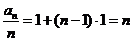 ,所以
,所以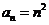 ,从而
,从而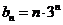
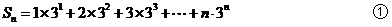
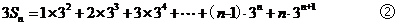
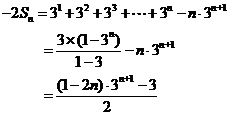 ①-②得:
①-②得:
所以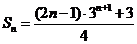
19
(Ⅰ)证:因为BC∥平面GEFH,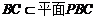 ,且
,且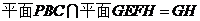 ,
,
所以GH∥BC。同理可证EF∥BC,因此GH∥EF。
(Ⅱ)解:连接AC,BD交于点O,BD交EF于点K,连接OP,GK
因为PA=PC,O是AC的中点,所以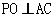 ,同理可得
,同理可得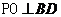
又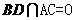 ,且AC、BD都在底面内,所以
,且AC、BD都在底面内,所以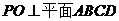
又因为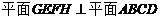 且
且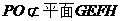 ,所以
,所以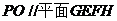 ,
,
因为
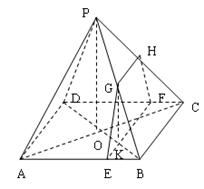 所以PO ∥GK,且
所以PO ∥GK,且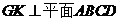 ,从而
,从而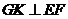 。
。
所以GK是梯形GEFH的高
由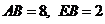 得
得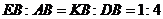
从而 ,即K为OB的中点。
,即K为OB的中点。
再由PO∥GK得,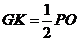 ,即G为PB的中点,且
,即G为PB的中点,且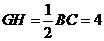
由已知可得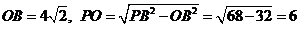
所以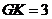
故四边形GEFH的面积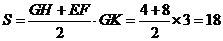 。
。
20
解:(Ⅰ) 的定义域为
的定义域为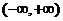 ,
,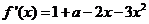
令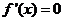 得
得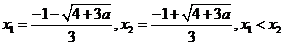
所以
当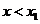 或
或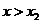 时
时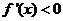 ;当
;当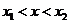 时
时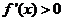
故 在
在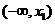 和
和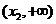 内单调递减,在
内单调递减,在 内单调递增。
内单调递增。
(Ⅱ)∵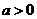 ,∴
,∴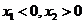
(1)当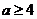 时
时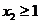 ,由(Ⅰ)知
,由(Ⅰ)知 在
在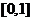 上单调递增
上单调递增
∴ 在
在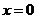 和
和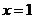 处分别取得最小值和最大值。
处分别取得最小值和最大值。
(2)当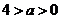 时,
时,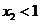 ,
,
由(Ⅰ)知 在
在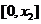 上单调递增,在
上单调递增,在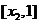 上单调递减
上单调递减
∴ 在
在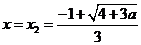 处取得最大值
处取得最大值
又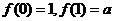
∴当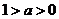 时
时 在
在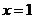 处取得最小值
处取得最小值
当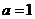 时
时 在
在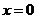 和
和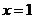 处同时取得最小值
处同时取得最小值
当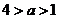 时,
时, 在
在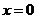 取得最小值。
取得最小值。
21
解:(Ⅰ)由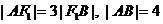 得
得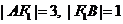 。
。
因为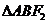 的周长为16,所以由椭圆定义可得
的周长为16,所以由椭圆定义可得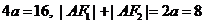
故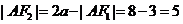 。
。
(Ⅱ)设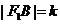 ,则
,则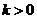 且
且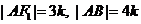 ,由椭圆定义可得
,由椭圆定义可得
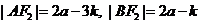
在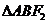 中,由余弦定理可得
中,由余弦定理可得
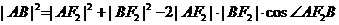
即
化简可得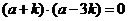 ,而
,而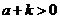 ,故
,故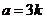
于是有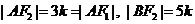 ,
,
因此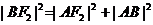 ,可得
,可得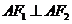
故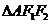 为等腰直角三角形。从而
为等腰直角三角形。从而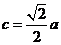
所以椭圆的离心率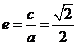 。
。
15. ①③④
14. 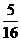
13. 4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com