
3.已知向量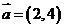 ,
, ,则
,则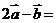 ( )
( )
A.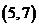 B.
B.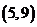 C.
C.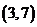 D.
D.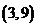
2.下列函数中,定义域是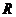 且为增函数的是( )
且为增函数的是( )
A.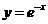 B.
B.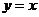 C.
C.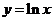 D.
D.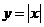
一、选择题共8小题,每小题5分,共40分。在每小题列出的4个选项中,选出符合题目要求的一项。
1.若集合 ,
,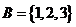 ,则
,则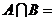 ( )
( )
A.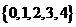 B.
B.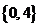 C.
C.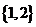 D.
D.
三、解答题:本大题共6小题,共75分.
(16)(本小题满分12分)
海关对同时从A,B,C三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如右表所示. 工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测.
|
地区 |
A |
B |
C |
|
数量 |
50 |
150 |
100 |
(I)求这6件样品中来自A,B,C各地区商品的数量;
(II)若在这6件样品中随机抽取2件送往甲机构进行进一步检测,求这2件商品来自相同地区的概率.
(17) (本小题满分12分)
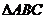 中,角A,B,C所对的边分别为
中,角A,B,C所对的边分别为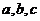 . 已知
. 已知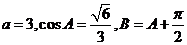 .
.
(I)求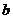 的值;
的值;
(II)求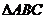 的面积.
的面积.
(18)(本小题满分12分)
如图,四棱锥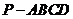 中,
中,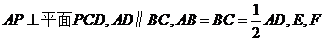 分别为线段
分别为线段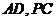 的中点.
的中点.

(I)求证: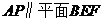 ;
;
(II)求证: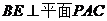 .
.
(19) (本小题满分12分)
在等差数列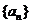 中,已知公差
中,已知公差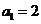 ,
,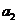 是
是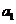 与
与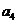 的等比中项.
的等比中项.
(I)求数列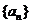 的通项公式;
的通项公式;
(II)设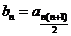 ,记
,记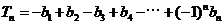 ,求
,求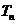 .
.
(20) (本小题满分13分)
设函数 ,其中
,其中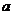 为常数.
为常数.
(I)若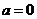 ,求曲线
,求曲线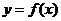 在点
在点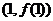 处的切线方程;
处的切线方程;
(II)讨论函数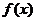 的单调性.
的单调性.
(21)(本小题满分14分)
在平面直角坐标系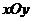 中,椭圆
中,椭圆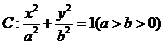 的离心率为
的离心率为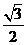 ,直线
,直线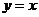 被椭圆
被椭圆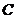 截得的线段长为
截得的线段长为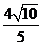 .
.
(I)求椭圆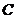 的方程;
的方程;
(II)过原点的直线与椭圆C交于A,B两点(A,B不是椭圆C的顶点). 点D在椭圆C上,且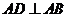 ,直线BD与
,直线BD与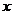 轴、
轴、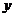 轴分别交于M,N两点.
轴分别交于M,N两点.
(i)设直线BD,AM的斜率分别为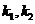 ,证明存在常数
,证明存在常数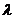 使得
使得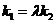 ,并求出
,并求出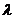 的值;
的值;
(ii)求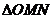 面积的最大值.
面积的最大值.
二、填空题:本大题共5小题,每小题5分,共25分.
 (11) 执行右面的程序框图,若输入的
(11) 执行右面的程序框图,若输入的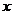 的值为1,则输出的
的值为1,则输出的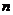 的值为 .
的值为 .
(12) 函数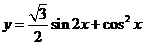 的最小正周期为
.
的最小正周期为
.
(13) 一个六棱锥的体积为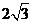 ,其底面是边长为2的正六边形,侧棱长都相等,则该六棱锥的侧面积为 。
,其底面是边长为2的正六边形,侧棱长都相等,则该六棱锥的侧面积为 。
(14) 圆心在直线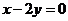 上的圆
上的圆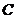 与
与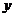 轴的正半轴相切,圆
轴的正半轴相切,圆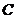 截
截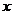 轴所得弦的长为
轴所得弦的长为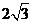 ,则圆
,则圆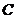 的标准方程为 。
的标准方程为 。
(15) 已知双曲线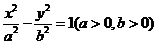 的焦距为
的焦距为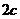 ,右顶点为A,抛物线
,右顶点为A,抛物线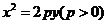 的焦点为F,若双曲线截抛物线的准线所得线段长为
的焦点为F,若双曲线截抛物线的准线所得线段长为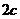 ,且
,且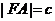 ,则双曲线的渐近线方程为 。
,则双曲线的渐近线方程为 。
一、选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的。
(1) 已知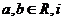 是虚数单位. 若
是虚数单位. 若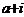 =
= ,则
,则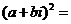
(A)
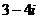 (B)
(B)
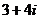 (C)
(C)
 (D)
(D)
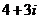
(2) 设集合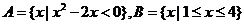 ,则
,则
(A)
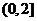 (B)
(B)
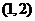 (C)
(C)
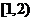 (D)
(D)
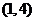
(3) 函数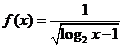 的定义域为
的定义域为
(A)
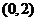 (B)
(B)
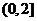 (C)
(C)
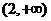 (D)
(D)
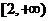
(4) 用反证法证明命题:“设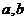 为实数,则方程
为实数,则方程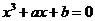 至少有一个实根”时,要做的假设是
至少有一个实根”时,要做的假设是
(A)
方程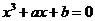 没有实根 (B)
方程
没有实根 (B)
方程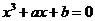 至多有一个实根
至多有一个实根
(C)
方程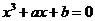 至多有两个实根 (D)
方程
至多有两个实根 (D)
方程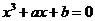 恰好有两个实根
恰好有两个实根
(5) 已知实数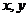 满足
满足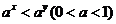 ,则下列关系式恒成立的是
,则下列关系式恒成立的是
(A)
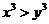 (B)
(B)
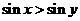
(C)
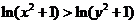 (D)
(D)
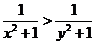
(6) 已知函数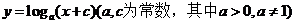 的图象如右图,则下列结论成立的是
的图象如右图,则下列结论成立的是

(A)
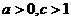 (B)
(B)
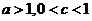
(C)
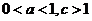 (D)
(D) 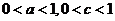
(7) 已知向量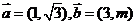 . 若向量
. 若向量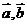 的夹角为
的夹角为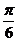 ,则实数
,则实数
(A)
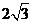 (B)
(B)
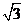 (C)
0 (D)
(C)
0 (D)
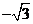
(8) 为了研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:kPa)的分组区间为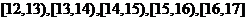 ,将其按从左到右的顺序分别编号为第一组,第二组,……,第五组,右图是根据试验数据制成的频率分布直方图。已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为
,将其按从左到右的顺序分别编号为第一组,第二组,……,第五组,右图是根据试验数据制成的频率分布直方图。已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为
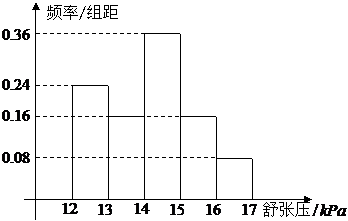

(A) 6
(B) 8
(C) 12
(D) 18
(9) 对于函数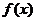 ,若存在常数
,若存在常数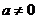 ,使得
,使得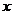 取定义域内的每一个值,都有
取定义域内的每一个值,都有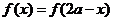 ,则称
,则称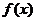 为准偶函数,下列函数中是准偶函数的是
为准偶函数,下列函数中是准偶函数的是
(A)
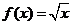 (B)
(B)
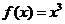
(C)
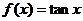 (D)
(D)
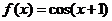
(10) 已知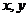 满足约束条件
满足约束条件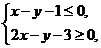 当目标函数
当目标函数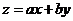
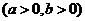 在该约束条件下取到最小值
在该约束条件下取到最小值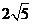 时,
时,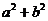 的最小值为
的最小值为
(A) 5 (B)
4 (C)
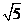 (D)
2
(D)
2
第II卷(共100分)
21.(满分14分)随机将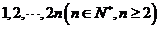 这2n个连续正整数分成A,B两组,每组n个数,A组最小数为
这2n个连续正整数分成A,B两组,每组n个数,A组最小数为 ,最大数为
,最大数为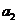 ;B组最小数为
;B组最小数为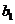 ,最大数为
,最大数为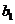 ,记
,记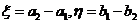
(1)当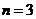 时,求
时,求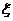 的分布列和数学期望;
的分布列和数学期望;
(2)令C表示事件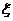 与
与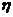 的取值恰好相等,求事件C发生的概率
的取值恰好相等,求事件C发生的概率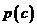 ;
;
(3)对(2)中的事件C, 表示C的对立事件,判断
表示C的对立事件,判断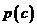 和
和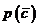 的大小关系,并说明理由。
的大小关系,并说明理由。
20.(本小题满分13分)
如图,已知双曲线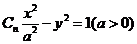 的右焦点
的右焦点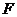 ,点
,点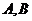 分别在
分别在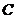 的两条渐近线上,
的两条渐近线上,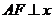 轴,
轴,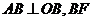 ∥
∥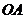 (
(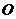 为坐标原点).
为坐标原点).
(1)求双曲线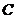 的方程;
的方程;
(2)过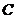 上一点
上一点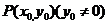 的直线
的直线 与直线
与直线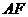 相交于点
相交于点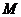 ,与直线
,与直线 相交于点
相交于点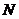 ,证明点
,证明点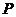 在
在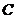 上移动时,
上移动时,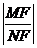 恒为定值,并求此定值
恒为定值,并求此定值
18、(本小题满分12分)
已知函数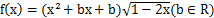 .
.
(1) 当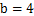 时,求
时,求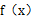 的极值;
的极值;
(2) 若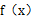 在区间
在区间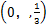 上单调递增,求b的取值范围.
上单调递增,求b的取值范围.
19(本小题满分12分)
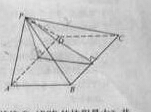
如图,四棱锥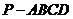 中,
中,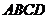 为矩形,平面
为矩形,平面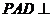 平面
平面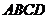 .
.
(1)求证: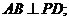
(2)若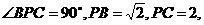 问
问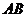 为何值时,四棱锥
为何值时,四棱锥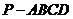 的体积最大?并求此时平面
的体积最大?并求此时平面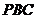 与平面
与平面 夹角的余弦值.
夹角的余弦值.
17、(本小题满分12分)
已知首项都是1的两个数列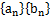 (
(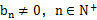 ),满足
),满足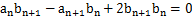 .
.
(1) 令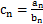 ,求数列
,求数列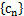 的通项公式;
的通项公式;
(2) 若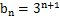 ,求数列
,求数列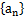 的前n项和
的前n项和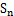 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com