
一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合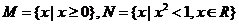 ,则
,则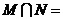 ( )
( )
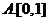
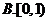
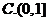
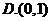
(二)选考题
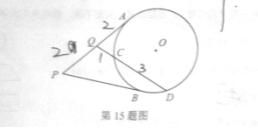
15.(选修4-1:几何证明选讲)
如图,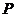 为⊙
为⊙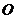 的两条切线,切点分别为
的两条切线,切点分别为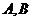 ,过
,过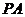 的中点
的中点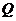 作割线交⊙
作割线交⊙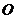 于
于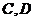 两点,若
两点,若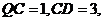 则
则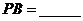
16.(选修4-4:坐标系与参数方程)
已知曲线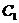 的参数方程是
的参数方程是
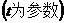 ,以坐标原点为极点,
,以坐标原点为极点,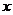 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线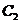 的极坐标方程是
的极坐标方程是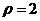 ,则
,则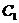 与
与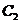 交点的直角坐标为________
交点的直角坐标为________
17、(本小题满分11分)
某实验室一天的温度(单位: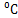 )随时间
)随时间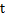 (单位;h)的变化近似满足函数关系;
(单位;h)的变化近似满足函数关系;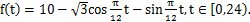
(1) 求实验室这一天的最大温差;
(2) 若要求实验室温度不高于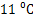 ,则在哪段时间实验室需要降温?
,则在哪段时间实验室需要降温?
18(本小题满分12分)
已知等差数列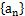 满足:
满足: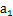 =2,且
=2,且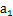 ,
,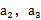 成等比数列.
成等比数列.
(1)
求数列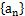 的通项公式.
的通项公式.
(2)
记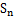 为数列
为数列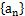 的前n项和,是否存在正整数n,使得
的前n项和,是否存在正整数n,使得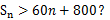 若存在,求n的最小值;若不存在,说明理由.
若存在,求n的最小值;若不存在,说明理由.
19(本小题满分12分)
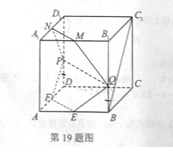
如图,在棱长为2的正方体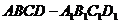 中,
中,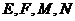 分别是棱
分别是棱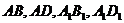 的中点,点
的中点,点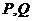 分别在棱
分别在棱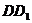 ,
,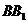 上移动,且
上移动,且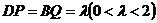 .
.
(1)当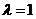 时,证明:直线
时,证明:直线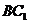 平面
平面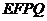 ;
;
(2)是否存在 ,使平面
,使平面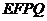 与面
与面 所成的二面角?若存在,求出
所成的二面角?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
20.(本小题满分12分)
计划在某水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水库年入流量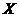 (年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(1)求未来4年中,至多1年的年入流量超过120的概率;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量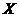 限制,并有如下关系;
限制,并有如下关系;

若某台发电机运行,则该台年利润为5000万元;若某台发电机未运行,则该台年亏损800万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
21.(满分14分)在平面直角坐标系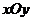 中,点M到点
中,点M到点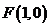 的距离比它到
的距离比它到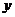 轴的距离多1,记点M的轨迹为C.
轴的距离多1,记点M的轨迹为C.
(1)求轨迹为C的方程
(2)设斜率为k的直线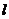 过定点
过定点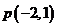 ,求直线
,求直线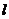 与轨迹C恰好有一个公共点,两个公共点,三个公共点时k的相应取值范围。
与轨迹C恰好有一个公共点,两个公共点,三个公共点时k的相应取值范围。
10.已知函数f(x)是定义在R上的奇函数,当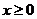 时,
时, 若
若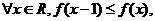 则实数a的取值范围为( )
则实数a的取值范围为( )
A.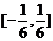 B.
B.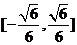 C.
C. 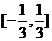 D.
D.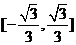
9.已知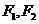 是椭圆和双曲线的公共焦点,
是椭圆和双曲线的公共焦点,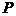 是他们的一个公共点,且
是他们的一个公共点,且 ,则椭圆和双曲线的离心率的倒数之和的最大值为( )
,则椭圆和双曲线的离心率的倒数之和的最大值为( )
A. B.
B.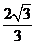 C.3 D.2
C.3 D.2
8.《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“盖”的术:置如其周,令相承也.又以高乘之,三十六成一.
该术相当于给出了有圆锥的底面周长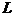 与高
与高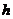 ,计算其体积
,计算其体积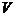 的近似公式
的近似公式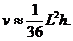 它实际上是将圆锥体积公式中的圆周率
它实际上是将圆锥体积公式中的圆周率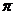 近似取为3.那么近似公式
近似取为3.那么近似公式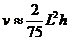 相当于将圆锥体积公式中的
相当于将圆锥体积公式中的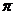 近似取为( )
近似取为( )
A.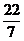 B.
B.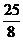 C.
C.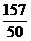 D.
D.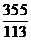
7.由不等式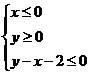 确定的平面区域记为
确定的平面区域记为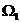 ,不等式
,不等式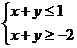 ,确定的平面区域记为
,确定的平面区域记为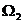 ,在
,在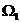 中随机取一点,则该点恰好在
中随机取一点,则该点恰好在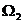 内的概率为( )
内的概率为( )
A.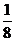 B.
B.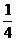 C.
C. 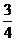 D.
D.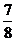
6.若函数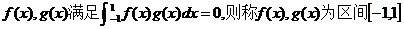 上的一组正交函数,给出三组函数:
上的一组正交函数,给出三组函数:
①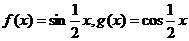 ;②
;②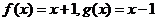 ;③
;③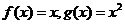
其中为区间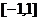 的正交函数的组数是( )
的正交函数的组数是( )
A.0 B.1 C.2 D.3
5.在如图所示的空间直角坐标系 中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),
中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),
(1,2,1),(2,2,2),给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为( )
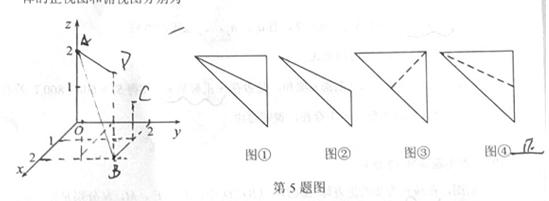
A. ①和② B.③和① C. ④和③ D.④和②
4.根据如下样本数据
|
x |
3 |
4 |
5 |
6 |
7 |
8 |
|
y |
4.0 |
2.5 |
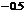 |
0.5 |
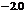 |
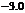 |
得到的回归方程为 ,则( )
,则( )
A.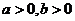 B.
B.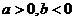 C.
C.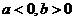 D.
D.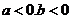
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com