
20.(1)设该城市人口总数为a,则该城市人均GDP为
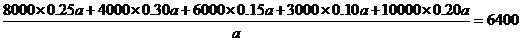
因为 ,
,
所以该城市人均GDP达到了中等偏上收入国家标准.
(2)“从5个行政区中随机抽取2个”的所有的基本事件是:
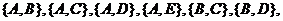
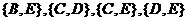 共10个,
共10个,
设事件“抽到的2个行政区人均GDP都达到中等偏上收入国家标准”为M,
则事件M包含的基本事件是: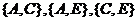 ,共3个,
,共3个,
所以所求概率为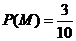 .
.
19.
(1)∵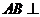 平面BCD,
平面BCD,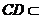 平面BCD,
平面BCD,
∴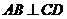 .
.
又∵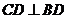 ,
,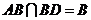 ,
,
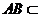 平面ABD,
平面ABD,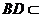 平面ABD,
平面ABD,
∴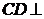 平面
平面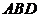 .
.
(2)由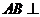 平面BCD,得
平面BCD,得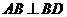 .
.
∵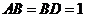 ,∴
,∴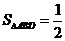 .
.
∵M是AD的中点,
∴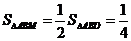 .
.
由(1)知,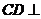 平面ABD,
平面ABD,
∴三棱锥C-ABM的高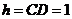 ,
,
因此三棱锥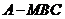 的体积
的体积
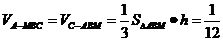 .
.
解法二:
(1)同解法一.
(2)由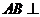 平面BCD知,平面ABD
平面BCD知,平面ABD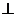 平面BCD,
平面BCD,
又平面ABD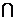 平面BCD=BD,
平面BCD=BD,
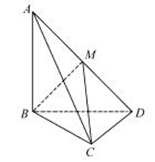
如图,过点M作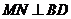 交BD于点N.
交BD于点N.
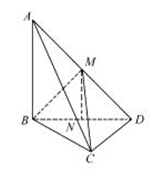
则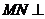 平面BCD,且
平面BCD,且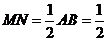 ,
,
又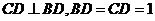 ,
,
∴ .
.
∴三棱锥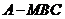 的体积
的体积
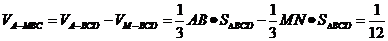 .
.
18.解法一:(1)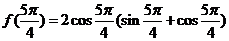
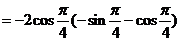
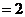
(2)因为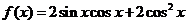
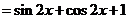
 .
.
所以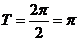 .
.
由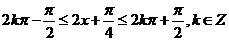 ,
,
得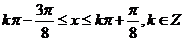 ,
,
所以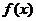 的单调递增区间为
的单调递增区间为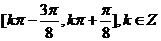 .
.
解法二:
因为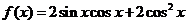
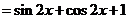

(1)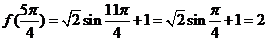
(2)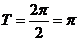
由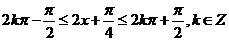 ,
,
得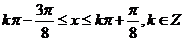 ,
,
所以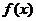 的单调递增区间为
的单调递增区间为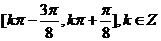 .
.
三.解答题:本大题共6小题,共74分.
17. (1)设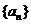 的公比为q,依题意得
的公比为q,依题意得
 ,
,
解得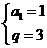 ,
,
因此,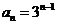 .
.
(2)因为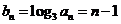 ,
,
所以数列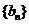 的前n项和
的前n项和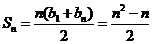 .
.
16. 
15. 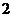
14. 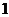
二、填空题
13. 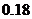
一.选择题
ABABCDDBCDCA
22.(本小题满分12分)
已知函数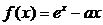 (
(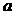 为常数)的图像与
为常数)的图像与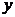 轴交于点
轴交于点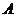 ,曲线
,曲线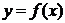 在点
在点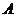 处的切线斜率为
处的切线斜率为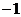 .
.
(Ⅰ)求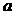 的值及函数
的值及函数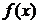 的极值;
的极值;
(Ⅱ)证明:当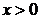 时,
时,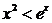
(Ⅲ)证明:对任意给定的正数c,总存在 ,使得当
,使得当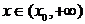 时,恒有
时,恒有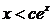
2014年普通高等学校招生全国统一考试(福建卷)
数学(文科)答案
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com