4.命题“垂直于同一条直线的两条直线互相平行”的题设是　　　　　　　 （　 ）．

（A）垂直　　　　 （B）两条直线

（C）同一条直线　 （D）两条直线垂直于同一条直线

3.不等式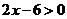的解集在数轴上表示正确的是　　　　　　　　　　　 (　　 )

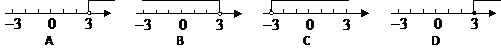
2．若a＞b，则下列式子正确的是　　　　　　　　　　　　　　　 　　( 　　) ．

A．a－6＞b－2　　　 B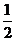．a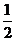＜b　　 C．4+3a＞4+3b　　 D．—2a＞—2b

一、选择题（共10小题，每小题3分，共30分；

1、方程2x-3y=5,x+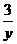=6,3x-y+2z=0,2x+4y,5x-y>0中是二元一次方程的有（）个。

A.1　　　　 B.2　　　　 C.3　　　　 D.4

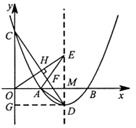
22.（满分14分）如图，抛物线y=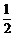(x-3)²-1与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，顶点为D了.

（1）求点A，B，D的坐标；

（2）连接CD，过原点O作OE⊥CD，垂足为H，OE与抛物线的对称轴交于点E，连接AE，AD.求证：∠AEO=∠ADC；

（3）以（2）中的点E为圆心，1为半径画圆，在对称轴右侧的抛物线上有一动点P，过点P作⊙E的切线，切点为Q，当PQ的长最小时，求点P的坐标，并直接写出点Q的坐标.

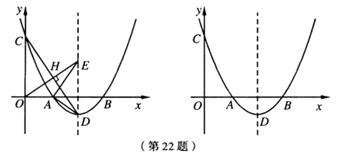
[答案]（1）顶点D的坐标为（3，-1）.

令y=0，得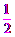(x-3)²-1=0，

解得x₁=3+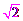，x₂=3-.

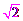∵点A在点B的左侧，

∴A点坐标(3-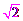，0)，B点坐标（3+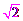，0）.

（2）过D作DG⊥y轴，垂足为G.

则G（0，-1），GD=3.

令x=0，则y=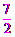，∴C点坐标为（0，）.

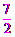∴GC=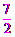-(-1)=.

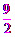设对称轴交x轴于点M.

∵OE⊥CD，

∴∠GCD+∠COH=90°.

∵∠MOE+∠COH=90°，

∴∠MOE=∠GCD.

又∵∠CGD=∠OMN=90°，

∴△DCG∽△EOM.

∴.

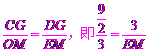∴EM=2，即点E坐标为(3，2)，ED=3.

由勾股定理，得AE²=6，AD²=3，

∴AE²+AD²=6+3=9=ED².

∴△AED是直角三角形，即∠DAE=90°.

设AE交CD于点F.

∴∠ADC+∠AFD=90°.

又∵∠AEO+∠HFE=90°，

∴∠AFD=∠HFE，

∴∠AEO=∠ADC.

（3）由⊙E的半径为1，根据勾股定理，得PQ²=EP²-1.

要使切线长PQ最小，只需EP长最小，即EP²最小.

设P坐标为（x，y），由勾股定理，得EP²=(x-3)²+(y-2)².

∵y=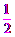(x-3)²-1，

∴(x-3)²=2y+2.

∴EP²=2y+2+y²-4y+4

　　 =(y-1)²+5.

当y=1时，EP²最小值为5.

把y=1代入y=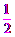(x-3)²-1，得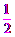(x-3)²-1=1，

解得x₁=1，x₂=5.

又∵点P在对称轴右侧的抛物线上，

∴x₁=1舍去.

∴点P坐标为(5，1).

此时Q点坐标为（3，1）或().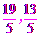　　

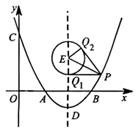
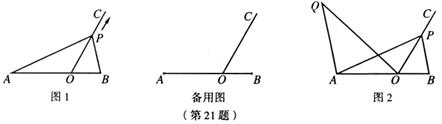
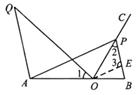
21．（满分13分）如图1，点O在线段AB上，AO=2，OB=1，OC为射线，且∠BOC=60°，动点P以每秒2个单位长度的速度从点O出发，沿射线OC做匀速运动，设运动时间为t秒.

（1）当t=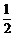秒时，则OP=　　　 ，S_△ABP=　　　　　　 ；

（2）当△ABP是直角三角形时，求t的值；

（3）如图2，当AP=AB时，过点A作AQ∥BP，并使得∠QOP=∠B，求证：AQ·BP=3.

[答案]解：（1）1，；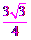

（2）①∵∠A<∠BOC=60°，

∴∠A不可能是直角.

②当∠ABP=90°时，

∵∠BOC=60°，

∴∠OPB=30°.

∴OP=2OB，即2t=2.

∴t=1.

③当∠APB=90°时，作PD⊥AB，垂足为D，则∠ADP=∠PDB=90°.

∵OP=2t，

∴OD=t，PD=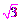t，AD=2+t，BD=1-t（△BOP是锐角三角形）.

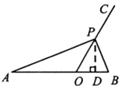
解法一：∴BP²=（1-t）² +3t²，AP²=(2+t)²+3t².

∵BP²+AP²=AB²，

∴(1-t)²+3t²+(2+t)²+3t²=9，

即4t²+t-2=0.

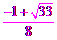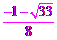解得t₁=，t₂= （舍去）.

解法二：∵∠APD+∠BPD=90°，∠B+∠BPD=90°，

∴∠APD=∠B.

∴△APD∽△PBD.

∴　

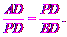
∴PD²=AD·BD.

于是(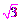t)²=(2+t)(1-t)，即 4t²+t-2=0.

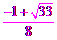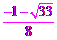解得t₁=，t₂= （舍去）.

综上，当△ABP为直角三角形时，t=1或.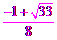

（3）解法一：∵AP=AB，

∴∠APB=∠B.

作OE∥AP，交BP于点E，

∴∠OEB=∠APB=∠B.

∵AQ∥BP，

∴∠QAB+∠B=180°.

又∵∠3+∠OEB=180°，

∴∠3=∠QAB.

又∵∠AOC=∠2+∠B=∠1+∠QOP，

已知∠B=∠QOP，

∴∠1=∠2.

∴△QAO∽△OEP.

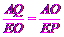∴，即AQ·EP=EO·AO.

∵OE∥AP，

∴△OBE∽△ABP.

∴.

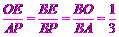
∴OE=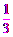AP=1，B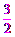P=EP.

∴AQ·BP=AQ·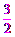EP=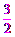AO·OE=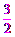´2´1=3.

解法二：连接PQ，设AP与OQ相交于点F.

∵AQ∥BP，

∴∠QAP=∠APB.

∵AP=AB，

∴∠APB=∠B.

∴∠QAP=∠B.

又∵∠QOP=∠B，

∴∠QAP=∠QOP.

∵∠QFA=∠PFO，

∴△QFA∽△PFO.

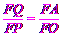∴，即.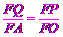

又∵∠PFQ=∠OFA，

∴△PFQ∽△OFA.

∴∠3=∠1.

∵∠AOC=∠2+∠B=∠1+∠QOP，

已知∠B=∠QOP，

∴∠1=∠2.

∴∠2=∠3.

∴△APQ∽△BPO.

∴.

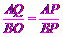∴AQ·BP=AP·BO=3´1=3.　 　

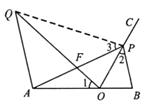
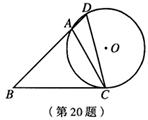
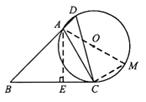
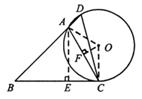
20．（满分11分）如图，在△ABC中，∠B=45°，∠ACB=60°，AB=3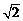，点D为BA延长线上的一点，且∠D=∠ACB，⊙O为△ACD的外接圆.

（1）求BC的长；

（2）求⊙O的半径.

[答案]解：（1）过点A作AE⊥BC，垂足为E.

∴∠AEB=∠AEC=90°.

在Rt△ABE中，∵sinB=，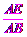

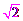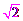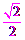∴AB=AB·sinB=3·sin45°= 3·=3.

∵∠B=45°，

∴∠BAE=45°.

∴BE=AE=3.

在Rt△ACE中，∵tan∠ACB=，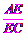

∴EC=.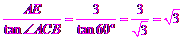

∴BC=BE+EC=3+.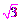

（2）由（1）得，在Rt△ACE中，∵∠EAC=30°，EC=，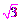

∴AC=2.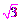

解法一：连接AO并延长交⊙O于M，连接CM.

∵AM为直径，

∴∠ACM=90°.

在Rt△ACM中，∵∠M=∠D=∠ACB=60°，sinM=，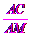

∴AM===4.

∴⊙O的半径为2.

解法二：连接OA，OC，过点O作OF⊥AC，垂足为F，

则AF=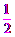AC=.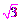

∵∠D=∠ACB=60°，

∴∠AOC=120°.

∴∠AOF=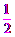∠AOC=60°.

在Rt△OAF中，sin∠AOF=，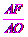

∴AO=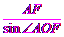=2，即⊙O的半径为2.　 　

19．（满分12分）现有A，B两种商品，买2件A商品和1件B商品用了90元，买3件A商品和2件B商品共用了160元.

（1）求A，B两种商品每件多少元？

（2）如果小亮准备购买A，B两种商品共10件，总费用不超过350元，且不低于300元，问有几种购买方案，哪种方案费用最低？

[答案]解：（1）设A商品每件x元，B商品每件y元.

依题意，得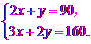　

解得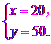

答：A商口每件20元，B商品每件50元.

（2）设小亮准备购买A商品a件，则购买B商品(10-a)件.

依题意，得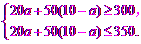　

解得5≤a≤6.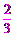

根据题意，a的值应为整数，所以a=5或a=6.

方案一：当a=5时，购买费用为20´5+50´(10-5)=350元；

方案二：当a=6时，购买费用为20´6+50´(10-6)=320元.

∵350>320，

∴购买A商品6件，B商品4件的费用最低.

答：有两种购买方案，方案一：购买A商品5件，B商品5件；方案二：购买A商品6件，B商品4件.其中方案二费用最低.

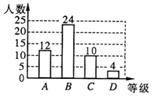
18．（满分12分）设中学生体质健康综合评定成绩为x分，满分为100分.规定：85≤x≤100为A级，75≤x<85为B级，60≤x<75为C级，x<60为D级.现随机抽取福海中学部分学生的综合评定成绩，整理绘制成如下两幅不完整的统计图.请根据图中的信息，解答下列问题：

　 （1）在这次调查中，一共抽取了　　　　　 名学生，a=　　　　 %；

（2）补全条形统计图；

（3）扇形统计图中C级对应的圆心角为　　　　　　 度；

（4）若该校共有2000名学生，请你估计该校D级学生有多少名？

[答案]解：（1）50，24；

（2）如图所示；

（3）72；

（4）该校D级学生有：2000´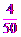=160人.

17．（每小题7分，共14分）

（1）如图，点E，F在BC上，BE=CF，AB=DC，∠B=∠C.求证：∠A=∠D.

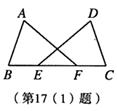
[答案]证明：∵BE=CF，

　　　　 ∴BE+EF=CF+EF

　　　　 即BF=CE.

　　　　 又∵AB=DC，∠B=∠C，

　　　　 ∴△ABF≌△DCE.

∴∠A=∠E.

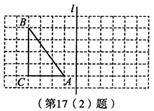
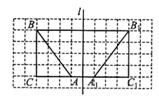
（2）如图，在边长为1个单位长度的小正方形所组成的网格中，△ABC的顶点均在格点上.

　　 ①sinB的值是　　　　　　 ；

　　 ②画出△ABC关于直线l对称的△A₁B₁C₁（A与A₁，B与B₁，C与C₁相对应）.连接AA₁，BB₁，并计算梯形AA₁B₁B的面积.

　 [答案]①；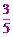

　 ②如图所示.

　 由轴对称的性质可得，AA₁=2，BB₁=8，高是4.

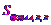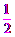　 ∴　=(AA₁+BB₁)´4=20.