
28.(12分)(1) 如图1,角∠MON=84°,点A、B分别在射线OM、ON上移动,△AOB的角平分线AC与BD交于点P.试问:随着点A、B位置的变化,∠APB的大小是否会变化?若保持不变,请求出∠APB的度数。若发生变化,请说明理由。
如图1,角∠MON=84°,点A、B分别在射线OM、ON上移动,△AOB的角平分线AC与BD交于点P.试问:随着点A、B位置的变化,∠APB的大小是否会变化?若保持不变,请求出∠APB的度数。若发生变化,请说明理由。
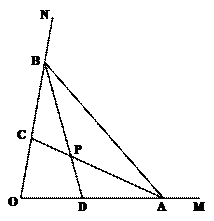 (2)如图2,两条互相垂直的直线MN、PQ,垂足为O,OE是∠PON的角平分线,点A、B分别在射线OE、OP上移动,BD是∠ABP的平分线,BD的反向延长线交∠OAB的平分线于点P,随着点A、B位置的变化,此时∠APB的大小是否会变化?若保持不变,请求出∠APB的度数。若发生变化,请说明理由。
(2)如图2,两条互相垂直的直线MN、PQ,垂足为O,OE是∠PON的角平分线,点A、B分别在射线OE、OP上移动,BD是∠ABP的平分线,BD的反向延长线交∠OAB的平分线于点P,随着点A、B位置的变化,此时∠APB的大小是否会变化?若保持不变,请求出∠APB的度数。若发生变化,请说明理由。

(图1) (图2)
 友情提醒:做完了,请仔细检查,不要留下遗憾噢!!
友情提醒:做完了,请仔细检查,不要留下遗憾噢!!
大丰市实验初级中学2013-2014学年度第二学期
27.乘法公式的探究及应用.(本题共12分)
探究活动:(1)如图1,可以求出阴影部分的面积是 ▲ (写成两数平方差的形式);
 (2)如图2,若将阴影部分裁剪下来,重新拼成一个长方形,面积是 ▲ (写成多项式乘法的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个长方形,面积是 ▲ (写成多项式乘法的形式);
(3)比较图1、图2阴影部分的面积,可以得到公式 ▲ ;
知识应用:运用你所得到的公式解决以下问题
(1)
计算: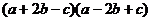
(2) 若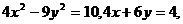 求
求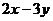 的值.
的值.
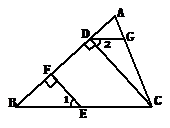
26. ( 10分) 如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,
(1)试判断DG与BC的位置关系,并说明理由。
(2)若∠A=70°,∠BCG=40°,求∠AGD的度数。
25.(本题共8分)一辆汽车从A地驶往B地,前三分之一路段为普通公路,其余路段为高速公路。已知汽车在普通公路上行驶的速度为60km/h,在高速公路上行驶的速度为1 00km/h,汽车从A地到B地一共行驶了2.2h。
00km/h,汽车从A地到B地一共行驶了2.2h。
 请你根据以上信息,就该汽车行驶的“路程”或“时间”,提出一个用二元一次方程组解 决的问题,并写出解答过程。
请你根据以上信息,就该汽车行驶的“路程”或“时间”,提出一个用二元一次方程组解 决的问题,并写出解答过程。
24. (本题10分)
若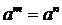 (
(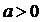 且
且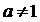 ,
,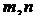 是正整数,则
是正整数,则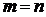 ,你能利用上面的结论解决下面的2个问题吗?试试看,相信你一定行!
,你能利用上面的结论解决下面的2个问题吗?试试看,相信你一定行!
①如果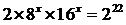 ,求
,求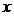 的值; ②如果
的值; ②如果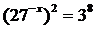 ,求
,求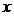 的值。
的值。
23.对于任意的有理数a、b、c、d,我们规定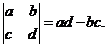 如:
如: 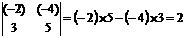 根据这一规定,解答下列问题:(本题8分)
根据这一规定,解答下列问题:(本题8分)
(1)化简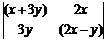
(2)若x、y同时满足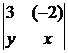 =6,
=6,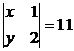 ,求x、y的值.
,求x、y的值.
22.(本题满分8分)
先化简,再求值:2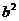 +(
+(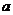 +
+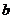 )(
)(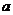 -2
-2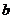 )-(
)-(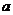 -
- ,其中
,其中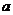 =-3,
=-3,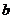 =
=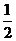 .
.
21. 分解因式(本题满分16分)
(1)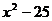 (2)
(2)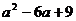
(3)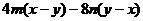 (4)
(4) 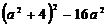
20. 计算(本题满分6分)
(1)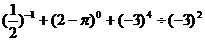 (2)用乘法公式简便计算:
(2)用乘法公式简便计算:
三.用心答一答
19.
(本题6分)在正方形网格中,每个 小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.
小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.
(1)请画出平移后的△A′B′C′
(2)若连接AA′,CC′,则这两条线段之间的关系是__▲ __.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com