1．从某一高度先后由静止释放两个相同的小球甲和乙，若两球被释放的时间间隔为1 s，在不计空气阻力的情况下，它们在空中运动的过程中(　)

A．甲、乙两球的距离越来越大，甲、乙两球的速度之差越来越大

B．甲、乙两球距离始终保持不变，甲、乙两球的速度之差保持不变

C．甲、乙两球距离越来越大，甲、乙两球的速度之差保持不变

D．甲、乙两球距离越来越小，甲、乙两球的速度之差越来越小

[解析]　甲、乙两球的距离Δs＝g(t＋1)²＝gt²＋gt＋g，所以越来越大．甲、乙两球的速度之差Δv＝g(t＋1)－gt＝g，所以不变．正确选项为C.

[答案]　C

2.一个固定在水平面上的光滑物块，其左侧面是斜面AB，右侧面是曲面AC，如图1－2所示．已知AB和AC的长度相同．两个小球p、q同时从A点分别沿AB和AC由静止开始下滑，比较它们到达水平面所用的时间(　)

图1－2

A．p小球先到　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B．q小球先到

C．两小球同时到　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．无法确定

[解析]　可以利用v－t图象(这里的v是速率，曲线下的面积表示路程)定性地进行比较．在同一个v－t图象中作出p、q的速率图线，如图所示．显然开始时q的加速度较大，斜率较大；由于机械能守恒，末速率相同，即两图线末端在同一水平线上．为使路程相同(两图线和横轴所围的面积相同)，显然q用的时间较少，故B正确．

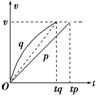
[答案]　B

巧选参照系，妙解运动题

　(多选)甲、乙两物体同时、同向且沿同一直线运动．乙在前面做初速度为0、加速度为a₂的匀加速运动，甲在后面做初速度为v₀、加速度为a₁的匀加速运动，则(　)

A．若a₁＝a₂，则两物体只能相遇一次

B．若a₁>a₂，则两物体一定相遇两次

C．若a₁<a₂，则两物体不能相遇

D．若a₁<a₂，则两物体可能相遇两次或不能相遇

[技法攻略]　选择乙物体为参照系．如果a₁＝a₂，则物体甲相对物体乙做初速度为v₀的匀速直线运动，所以两物体只能相遇一次，A正确．如果a₁>a₂，则物体甲相对物体乙做初速度为v₀、加速度为(a₁－a₂)的匀加速运动，所以两物体只能相遇一次，B错误．如果a₁<a₂，则物体甲对物体乙做初速度为v₀、加速度为－(a₁－a₂)的匀减速运动．如果甲物体在追上乙物体之前速度减为0(即甲、乙两物体速度相等)，则两物体不能相遇；如果甲物体追上乙物体后速度减为0(即甲、乙两物体速度相等)，甲物体反向加速，再与乙物体相遇一次．所以D正确．故答案为A、D.

[答案]　AD

　A、B两车在同一直线上做同向匀速运动，A在前，速度为v_A＝8 m/s，B在后，速度为v_B＝16 m/s，当A、B相距x＝20 m时，B开始刹车，做匀减速运动，为避免A、B相撞，则刹车后B的加速度应为多大？

[技法攻略]　选A为参照系，则B相对于A的速度为v_B－v_A，为避免A、B相撞，B刹车后应满足：＜x

解得a＞1.6 m/s².

[答案]　B的加速度应大于1.6 m/s²

1．火车匀减速滑行，其前端通过信号灯时速度为v，末端恰好停于信号灯处，则前半列火车跟后半列火车通过信号灯的时间之比为(　)

A．1∶1　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.∶1

C．(－1)∶1　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．(＋1)∶1

[解析]　逆着车行方向，火车做初速度为零的匀加速运动，设加速度大小为a，火车全长为l，后半列火车逆向通过信号灯的时间为t₂，前半列火车逆向通过信号灯的时间为t₁，则有

＝at，l＝a(t₁＋t₂)²

联立可得t₁＋t₂＝t₂

所以＝，选项C正确．

[答案]　C

利用图象法处理非匀变速运动问题

对于物体的运动过程是变加速运动或曲线运动的问题，应从能量的角度对物体的运动过程进行分析，此时若直接从变速运动入手，则非常复杂，如果通过画运动图象辅助分析，结合图象与能量知识可方便求解．

　如图1－1所示，两物体由高度相同、路径不同的光滑斜面由静止下滑，物体通过两条路径的长度相等，通过C点前后速度大小不变，则下列说法正确的是(　)

A．物体沿AB斜面运动时间较短

B．物体沿ACD斜面运动时间较短

C．物体沿两个光滑斜面运动时间相等

D．无法确定

图1－1

[审题指导]　本题比较重要的条件有

(1)隐含条件：两过程中机械能均守恒，故末速度大小相等．

(2)路程条件：两过程中路径的长度相等，虽位移不同，可等效为位移的大小相等．

[解析]　由于两斜面光滑，且物体通过C点前后速度大小不变，说明整个过程机械能守恒，则两物体到达斜面最低点的速度大小相等，而且两物体运动路程相等，故可利用速度—时间图象进行分析比较．

从图中可以看出，沿AC段运动时，起始阶段加速度较大，故其速度图象起始阶段斜率较大，且二者末速度相等，为了保证最后速度大小一样且包围的面积(路程)一样，可以看到通过AB的时间t₁大于通过ACD的时间t₂，所以沿ACD斜面先到达，故B正确．

[答案]　B

[即学即用]

8．如图8甲所示，质量为m＝1 kg的物体置于倾角为θ＝37°的固定斜面上(斜面足够长)，对物体施加平行于斜面向上的恒力F，作用时间t₁＝1 s时撤去拉力，物体运动的部分v－t图象如图乙所示，取g＝10 m/s²，sin 37°＝0.6，cos 37°＝0.8.

甲　　　乙

图8

试求：

(1)物体与斜面间的动摩擦因数和拉力F的大小；

(2)t＝6 s时物体的速度，并在图乙上将6 s内物体运动的v－t图象补画完整，要求标明有关数据．

[解析]　(1)设撤去拉力前物体的加速度大小为a₁，撤去拉力后物体沿斜面继续上滑的加速度大小为a₂，由v－t图象可知：

a₁＝ m/s²＝20 m/s²

a₂＝m/s²＝10 m/s²

对物体在撤去拉力前，由牛顿第二定律得

F－mgsin 37°－μmgcos 37°＝ma₁

对物体在撤去拉力后上滑时，由牛顿第二定律得

mgsin 37°＋μmgcos 37°＝ma₂

解得F＝30 N，μ＝0.5.

(2)加速上滑的时间t₁＝1 s，撤去拉力时的速度为v＝20 m/s，设再经过时间t₂速度减至0.

由0＝v－a₂t₂得t₂＝2 s

在最高点时，因mgsin 37°>μmgcos 37°，

故物体将沿斜面加速下滑，设加速度大小为a₃，据牛顿第二定律得

mgsin 37°－μmgcos 37°＝ma₃

解得a₃＝2 m/s²

再经过3 s物体的速度大小为6 m/s，方向沿斜面向下，补画完整后的图线及有关数据如图所示．

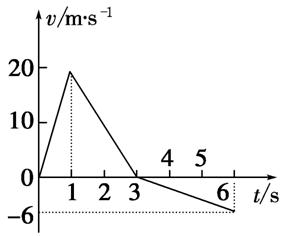
[答案]　(1)0.5　30 N　(2)见解析图

7．如图7所示，一块磁铁放在铁板ABC上的A处，其中AB长为1 m，BC长为0.6 m，BC与水平面夹角为37°，磁铁与铁板间的引力为磁铁重力的0.2倍，磁铁与铁板间的动摩擦因数μ＝0.25，现给磁铁一个水平向左的初速度v₀＝4 m/s不计磁铁经过B处转向的机械能损失．求：(sin 37°＝0.6，cos 37°＝0.8 g取10 m/s²)

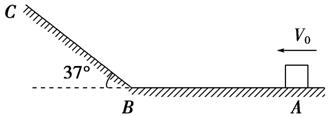
图7

(1)磁铁第一次到达B处的速度大小；

(2)磁铁沿BC向上运动的加速度大小；

(3)请通过计算判断磁铁最终能否再次回到B点．

[解析]　(1)N＝kmg＋mg＝1.2 mg

f＝μN＝0.25×1.2mg＝0.3mg

根据牛顿第二定律a₁＝＝3 m/s²

v_B＝＝ m/s≈3.16 m/s.

(2)磁铁沿BC向上运动时，N′－mgcos 37°－kmg＝0

μN′＋mgsin 37°＝ma₂

a₂＝＝＝8.5 m/s²

(3)磁铁沿BC向上运动的最大距离

s＝＝ m≈0.59 m<0.6 m

又因mgsin 37°>μ(mgcos 37°＋kmg)

所以磁块最终能再次回到B点．

[答案]　(1)3.16 m/s　(2)8.5 m/s²　(3)能回到B点

6．(多选)(2013·衡水中学调研)如图6所示，倾角为30°的光滑杆上套有一个小球和两根轻质弹簧，两弹簧的一端各与小球相连，另一端分别用销钉M、N固定于杆上，小球处于静止状态．设拔去销钉M(撤去弹簧a)瞬间，小球的加速度大小为6 m/s²，若不拔去销钉M，而拔去销钉N(撤去弹簧b)瞬间，小球的加速度可能是(g取10 m/s²)(　)

图6

A．11 m/s²，沿杆向上　　　　　　　　　　　　　　　　　　　　　　　 B．11 m/s²，沿杆向下

C．1 m/s²，沿杆向下　　　　　　　　　　　　　　　　　　　　　　　　 D．1 m/s²，沿杆向上

[解析]　设小球处于静止状态时b弹簧弹力为F，拔去销钉M瞬间，取向上为正方向，若a＝6 m/s²，由牛顿第二定律，F－mgsin 30°＝ma，解得F＝11m.若a＝－6 m/s²，由牛顿第二定律，－F－mgsin 30°＝ma，解得F＝m.

设a弹簧弹力为F′，由平衡条件F＝mgsin 30°＋F′，当F＝11m可得F′＝6m，拔去销钉N瞬间，由牛顿第二定律，F′＋mgsin 30°＝ma′，解得a′＝11 m/s²，选项B正确，A错误；当F＝m可得F′＝－4m，拔去销钉N瞬间，由牛顿第二定律，F′＋mgsin 30°＝ma′，解得a′＝1 m/s²，方向沿杆向下，选项C正确，D错误．

[答案]　BC

5.(多选)在光滑的水平面上有一个物体同时受到两个水平力F₁和F₂的作用，在第1 s内保持静止，若两力F₁和F₂随时间的变化图线如图5所示，则下列说法正确的是(　)

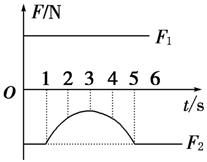
图5

A．在第2 s内物体做加速运动，加速度的大小逐渐减小，速度逐渐增大

B．在第3 s内物体做加速运动，加速度的大小逐渐减小，速度逐渐增大

C．在第4 s内物体做加速运动，加速度的大小逐渐减小，速度逐渐增大

D．在第5 s末，物体的加速度为零，运动方向与F₁相同

[解析]　由物体在第1 s内保持静止可知F₁和F₂的合力为零，即F₁与F₂大小相等，方向相反，在第2 s内和第3 s内F₂减小，F₁与F₂的合力增大，加速度大小逐渐增大，速度逐渐增大，A、B错误．第4 s内F₂逐渐增大，F₁与F₂的合力逐渐减小，加速度逐渐减小，速度逐渐增大，第5 s末F₁与F₂的合力为零，加速度为零，速度方向与F₁相同，C、D正确．

[答案]　CD

4.如图4所示，劲度系数为k的轻弹簧竖直固定在水平面上，上端固定一质量为m₀的托盘，托盘上有一个质量为m的木块．用竖直向下的力将原长为l₀的弹簧压缩后突然撤去外力，则m即将脱离m₀时的弹簧长度为(　)

A．l₀　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B．

C．l₀－　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．l₀－

图4

[解析]　弹簧上端只有托盘时，弹簧被压缩的长度为；当再加上木块时，弹簧被压缩的长度为；在力的作用下，弹簧被压缩的更多．撤去外力后，两者加速向上运动，当到达压缩量为时，速度达到最大而加速度为零，显然这时木块和托盘之间有压力作用，且压力等于木块的重力．再向上做减速运动，由于木块处于失重状态，对托盘的压力变小．当恰好分离时，两者恰好无相互作用力，两者都处于完全失重状态，所以弹簧为原长，选项A正确．

[答案]　A

3．(2013·安徽江南十校摸底)如图3所示，在动摩擦因数μ＝0.2的水平面上有一个质量m＝1 kg的小球，小球与水平轻弹簧及与竖直方向成θ＝45°角的不可伸长的轻绳一端相连，此时小球处于静止状态，且水平面对小球的弹力恰好为零．在剪断轻绳的瞬间(g取10 m/s²)，下列说法中正确的是

(　)

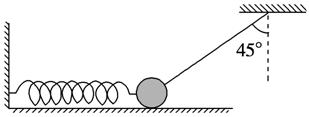
图3

A．小球受力个数不变

B．小球立即向左运动，且a＝8 m/s²

C．小球立即向左运动，且a＝10 m/s²

D．若剪断的是弹簧，则剪断瞬间小球加速度的大小a＝10 m/s²

[解析]　在剪断轻绳前，分析小球受力，小球受到重力、弹簧弹力和绳子拉力．应用平衡条件可得弹簧弹力F＝mgtan 45°＝10 N．剪断轻绳的瞬间，弹簧弹力不变，重力不变，小球将受到水平面的弹力和摩擦力，小球受力个数变化，选项A错误；此时在竖直方向，水平面的弹力N＝mg，摩擦力为f＝μN＝2 N，小球水平向左的合力F－f＝ma，解得a＝8 m/s²，选项B正确，C错误；若剪断的是弹簧，则剪断瞬间小球仍然静止，小球加速度的大小a＝0，选项D错误．

[答案]　B

2.(2014届沈阳一中模拟)如图2所示，质量为m₁＝2 kg的物体A经跨过定滑轮的轻绳与质量为M＝5 kg的箱子B相连，箱子底板上放一质量为m₂＝1 kg的物体C，不计定滑轮的质量和一切阻力，在箱子加速下落的过程中，取g＝10 m/s²，下列说法正确的是(　)

图2

A．物体A处于失重状态，加速度大小为10 m/s²

B．物体A处于超重状态，加速度大小为20 m/s²

C．物体C处于失重状态，对箱子的压力大小为5 N

D．轻绳对定滑轮的作用力大小为80 N

[解析]　取A、B、C为整体，由牛顿第二定律得(M＋m₂)g－m₁g＝(M＋m₁＋m₂)a，则加速度为a＝5 m/s²，A、B错；隔离C有m₂g－F_N＝m₂a，即F_N＝5 N，C对；隔离A有T－m₁g＝m₁a，即T＝30 N，所以轻绳对定滑轮的作用力大小为2T＝60 N，D错．

[答案]　C