4．如图5甲所示，理想变压器的原线圈匝数n₁＝350匝，副线圈匝数n₂＝70匝，电阻R＝20 Ω，是交流电压表，原线圈加上如图乙所示的交流电，则下列说法正确的是(　)

图5

A．加在原线圈上交流电压瞬时值的表达式为u＝20sin (5πt) V

B．原线圈电流的有效值为1 A

C．在t＝0.01s时，电压表的示数为0

D．电阻R上消耗的电功率为0.8 W

[解析]　由图乙可知，加在原线圈上交流电压瞬时值的表达式为u＝20sin (100πt) V，选项A错误；由变压器变压公式知，电压表读数为4 V，选项C错误．电阻R上电流i＝0.2 A，消耗的电功率为0.8 W，选项D正确．由输入功率等于输出功率可得原线圈电流的有效值为0.04 A，选项B错误．

[答案]　D

3．(2014·山东省青岛二中测试)图3、图4分别表示两种电压的波形，其中图1所示电压按正弦规律变化．下列说法正确的是(　)

A．图3表示交流电，图4表示直流电

B．两种电压的有效值相等

C．图3所示电压的瞬时值表达式为u＝311sin 100πt V

D．图3所示电压经匝数比为10∶1的变压器变压后，频率变为原来的

[解析]　交流电是电流大小和方向随时间发生变化的电流，两个图中都是交流电，A错；图3是正弦交流电，图4是锯齿形交流电，图形不同，有效值大小不相等，B错；由图3所提供的信息可知，C对；变压器不改变交流电的频率大小，D错．

[答案]　C

2．一理想变压器原、副线圈的匝数比n₁∶n₂＝2∶1，原线圈两端接正弦式交变电流，其电压u随时间t变化的规律如图2所示，则副线圈两端电压的有效值和频率分别为(　)

图2

A．110 V,50 Hz　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B．110 V,0.5 Hz

C．220 V,50 Hz　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．220 V,0.5 Hz

[解析]　变压器不改变交变电流的频率，由题u－t图象看出，该交变电压的周期T＝2×10^－2 s，故其频率f＝＝ Hz＝50 Hz；由u－t图象还可看出，该交变电压的最大值U_m＝311 V，故其有效值U＝＝ V≈220 V，代入变压器的变压比公式得副线圈两端电压的有效值U₂＝U₁＝U＝×220 V＝110 V，综上所述，正确选项为A.

[答案]　A

1．一个10 Ω的电阻，它两端的电压u随时间t的变化规律如图1所示，则(　)

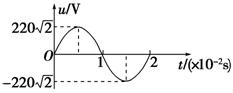
图1

A．流过电阻的最大电流是22 A

B．用交流电压表测量电阻两端的电压，其示数约为311 V

C．电阻消耗的功率为9 680 W

D．在交流电变化的前半个周期内，电阻产生的焦耳热是48.4 J

[解析]　电压峰值为220 V≈311 V，最大电流为 A＝31.1 A，电压有效值为220 V，电压表测的是有效值，电阻消耗的功率为P＝＝ W＝4 840 W，前半个周期电阻产生的焦耳热为Q＝P·＝48.4 J．因此只有选项D正确．

[答案]　D

2．如图10－4甲所示，理想变压器原、副线圈的匝数比为10∶1，R₁＝20 Ω，R₂＝30 Ω，C为电容器．已知通过R₁的正弦式交流电如图乙所示，则(　)

图10－4

A．交流电的频率为0.02 Hz

B．原线圈输入电压的最大值为200 V

C．电阻R₂的电功率约为6.67 W

D．通过R₃的电流始终为零

[解析]　由图乙可知交流电的周期为0.02 s，频率为50 Hz，所以A错．副线圈电压最大值U₂＝I_m1R₁＝20 V，由＝可知，原线圈电压的最大值U₁＝200 V，B错．R₁和R₂并联，P₂＝≈6.67 W，故C正确；因电容器接交流电有充放电电流，故D错．

[答案]　C

巧用变压器因果关系，妙解变压器动态问题

变压器中的“因果关系”是指原、副线圈中各物理量的制约关系．电压是原线圈决定副线圈，电流和功率是副线圈决定原线圈．解题中应牢记制约关系，不可颠倒．

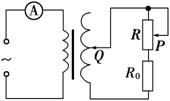
图10－5

(2014·惠州高二检测)一理想变压器的原线圈连接一只电流表，副线圈接入电路的匝数可以通过滑动触头Q调节，如图10－5所示，在副线圈上连接了定值电阻R₀和滑动变阻器R，P为滑动变阻器的滑动触头．原线圈两端接在电压为U的交流电源上．则(　)

A．保持Q的位置不动，将P向上滑动时，电流表的读数变大

B．保持Q的位置不动，将P向上滑动时，电流表的读数变小

C．保持P的位置不动，将Q向上滑动时，电流表的读数不变

D．保持P的位置不动，将Q向上滑动时，电流表的读数变小

[技法攻略]　Q位置不动，输出电压不变，P向上滑动，R阻值变大，输出电流变小，输入电流变小，电流表读数变小，选项A错，B对；P位置不动，R不变，Q向上滑动，输出电压变大，输出电流变大，输入电流变大，电流表读数变大，选项C、D错．

[答案]　B

　(多选)

图10－6

如图10－6所示，理想变压器的副线圈上通过输电线接有两个相同的灯泡L₁和L₂，输电线的等效电阻为R.开始时，开关S断开，当S接通时，以下说法正确的是(　)

A．副线圈两端M、N的输出电压减小

B．副线圈输电线等效电阻R上的电压增大

C．通过灯泡L₁的电流减小

D．原线圈中的电流增大

[技法攻略]　由于输入电压不变且原副线圈匝数不变，所以S接通时，理想变压器副线圈M、N两端输出电压不变，负载总电阻变小，由欧姆定律I＝知，流过R的电流增大，电阻上的电压降U_R＝IR增大；副线圈输出电流增大，根据输入功率等于输出功率，即I₁U₁＝I₂U₂得原线圈输入电流I₁也增大．U_MN不变，U_R变大，所以U_L1变小，流过灯泡L₁的电流减小．

[答案]　BCD

2．从图象获得的信息可以帮助我们求解有效值、书写交变电流瞬时值表达式等．

　(多选)(2014·山东青岛二中测试)一矩形线圈，在匀强磁场中绕垂直磁感线的对称轴转动，形成如图10－3所示的交变电动势图象，根据图象提供的信息，以下说法正确的是(　)

图10－3

A．线圈转动的角速度为 rad/s

B．电动势的有效值为14.1 V

C．t＝1.0×10^－2 s时，线圈平面和磁场方向的夹角为30°

D．t＝1.5×10^－2 s时，穿过线圈平面的磁通量最大

[解析]　角速度ω＝＝ rad/s，A项正确；电动势的有效值E＝＝14.1 V，B项正确；电动势的瞬时值e＝20sin t (V)，将t＝1.0×10^－2 s代入该式，解得θ＝，这是线圈从中性面开始转过的夹角，故线圈平面和磁场方向的夹角为30°，C项正确；t＝1.5×10^－2 s时，线圈平面与磁场平行，磁通量最小，D项错．

[答案]　ABC

[即学即用]

1.从交变电流的图象可以看出交流电的最大值、周期及交变电流的变化规律．

1．如图10－2所示为一交变电流随时间变化的图象，则此交变电流的有效值是多少？

图10－2

[解析]　交变电流的周期T＝0.02 s，在前半周期，电流为I₁＝4 A；后半周期电流I₂＝3 A

根据焦耳定律，在一个周期内交变电流通过电阻R产生的热量Q＝IR＋IR＝I²RT

故交变电流的有效值I＝＝5 A.

[答案]　5 A

用“数形结合”思想分析交变电流图象

2．对于非正弦式交变电流，可在一个周期内分段求出产生的热量，再求热量的总和Q.将总热量Q用相应的物理量I或U来表示(如Q＝I²Rt或Q＝t)，则I或U为其交变电流的相应有效值．

　如图10－1所示为一交变电流随时间变化的图象，从t＝0时刻开始，每半个周期时间内的图象均为正弦曲线，求此交变电流的有效值．

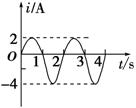
图10－1

[解析]　选择一个周期的时间，利用在相同时间内通过相同的电阻所产生的热量相同，由焦耳定律求得I²RT＝IR＋IR，其中I₁＝ A，I₂＝2 A，解得I＝ A.

[答案]　 A

[即学即用]

1.有效值是利用电流的热效应定义的，其中包含了“等效代替”的思想方法，即如果交流电通过电阻时产生的热量与直流电通过同一电阻在相同时间内产生的热量相等，则直流电的数值就是该交流电的有效值．用来计算电路中的电功率和电热．