四、解答题

20．（2014年广东汕尾）如图，在平行四边形ABCD中，E是AD边上的中点，连接BE，并延长BE交CD的延长线于点F．

（1）证明：FD=AB；

（2）当平行四边形ABCD的面积为8时，求△FED的面积．

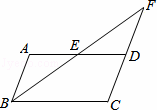
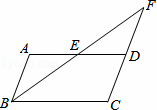
分析：（1）利用已知得出△ABE≌△DFE（AAS），进而求出即可；

（2）首先得出△FED∽△FBC，进而得出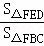=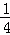，进而求出即可．

（1）证明：∵在平行四边形ABCD中，E是AD边上的中点，∴AE=ED，∠ABE=∠F，

在△ABE和△DFE中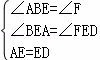，∴△ABE≌△DFE（AAS），∴FD=AB；

（2）解：∵DE∥BC，∴△FED∽△FBC，∵△ABE≌△DFE，

∴BE=EF，S_△FDE=S_{平行四边形ABCD}，∴=，∴=，∴=，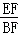

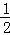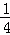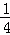∴△FED的面积为：2．

点评：　　 此题主要考查了全等三角形的判定与性质以及平行四边形的性质以及相似三角形的判定与性质等知识，得出S_△FDE=S_{平行四边形ABCD}是解题关键．

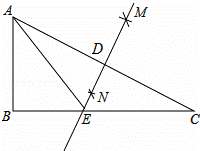
19．（2014年广东汕尾）如图，在Rt△ABC中，∠B=90°，分别以点A、C为圆心，大于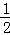AC长为半径画弧，两弧相交于点M、N，连接MN，与AC、BC分别交于点D、E，连接AE．

（1）求∠ADE；（直接写出结果）

（2）当AB=3，AC=5时，求△ABE的周长．

分析：（1）根据题意可知MN是线段AC的垂直平分线，由此可得出结论；

（2）先根据勾股定理求出BC的长，再根据线段垂直平分线的性质即可得出结论．

解：（1）∵由题意可知MN是线段AC的垂直平分线，∴∠ADE=90°；

（2）∵在Rt△ABC中，∠B=90°，AB=3，AC=5，∴BC=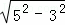=4，

∵MN是线段AC的垂直平分线，∴AE=CE，

∴△ABE的周长=AB+（AE+BE）=AB+BC=3+4=7．

点评：本题考查的是作图﹣基本作图，熟知垂直平分线上任意一点，到线段两端点的距离相等是解答此题的关键．

18．（2014年广东汕尾）已知反比例函数y=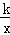的图象经过点M（2，1）

（1）求该函数的表达式；

（2）当2＜x＜4时，求y的取值范围（直接写出结果）．

分析：（1）利用待定系数法把（2，1）代入反比例函数y=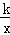中可得k的值，进而得到解析式；

（2）根据y=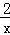可得x=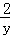，再根据条件2＜x＜4可得2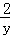＜＜4，再解不等式即可．

解：（1）∵反比例函数y=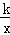的图象经过点M（2，1），∴k=2×1=2，

∴该函数的表达式为y=；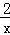

（2）∵y=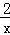，∴x=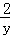，∵2＜x＜4，∴2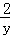＜＜4，解得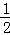：＜y＜1．

点评：此题主要考查了待定系数法求反比例函数解析式，以及反比例函数的性质，关键是正确确定函数解析式．

三、解答题

17．（（2014年广东汕尾）计算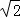：（+π）⁰﹣2|1﹣sin30°|+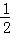（）^﹣1．

分析：原式第一项利用零指数幂法则计算，第二项利用特殊角的三角函数值及绝对值的代数意义化简，最后一项利用负指数幂法则计算即可得到结果．

解：原式=1﹣2×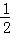+2=1﹣1+2=2．

点评：此题考查了实数的运算，熟练掌握运算法则是解本题的关键．

16．（2014年广东汕尾）如图，把△ABC绕点C按顺时针方向旋转35°，得到△A′B′C，A′B′交AC于点D．若∠A′DC=90°，则∠A=　．

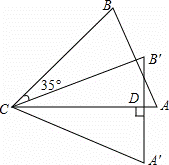
分析：　　 根据题意得出∠ACA′=35°，则∠A′=90°﹣35°=55°，即可得出∠A的度数．

解：∵把△ABC绕点C按顺时针方向旋转35°，得到△A′B′C，A′B′交AC于点D，∠A′DC=90°，∴∠ACA′=35°，则∠A′=90°﹣35°=55°，

则∠A=∠A′=55°．故答案为：55°．

点评：此题主要考查了旋转的性质以及三角形内角和定理等知识，得出∠A′的度数是解题关键．

15．（2014年广东汕尾）写出一个在三视图中俯视图与主视图完全相同的几何体　．

分析：主视图、俯视图是分别从物体正面和上面看，所得到的图形．

解：球的俯视图与主视图都为圆；正方体的俯视图与主视图都为正方形．

故答案为：球或正方体．

点评：考查学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．

14．（2014年广东汕尾）小明在射击训练中，五次命中的环数分别为5、7、6、6、6，则小明命中环数的众数为　，平均数为　．

分析：根据众数和平均数的概念求解．

解：6出现的次数最多，故众数为6，平均数为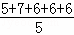：=6．故答案为：6，6．

点评：本题考查了众数和平均数的概念：一组数据中出现次数最多的数据叫做众数；平均数是指在一组数据中所有数据之和再除以数据的个数．

13．（2014年广东汕尾）已知a，b，c为平面内三条不同直线，若a⊥b，c⊥b，则a与c的位置关系是　．

分析：根据在同一平面内，如果两条直线同时垂直于同一条直线，那么这两条直线平行可得答案．

解：∵a⊥b，c⊥b，∴a∥c，故答案为：平行．

点评：此题主要考查了平行线的判定，关键是掌握在同一平面内，如果两条直线同时垂直于同一条直线，那么这两条直线平行．

12．（2014年广东汕尾）已知a+b=4，a﹣b=3，则a²﹣b²=　．

分析：根据a²﹣b²=（a+b）（a﹣b），然后代入求解．

解：a²﹣b²=（a+b）（a﹣b）=4×3=12．故答案是：12．

点评：本题重点考查了用平方差公式．平方差公式为（a+b）（a﹣b）=a²﹣b²．本题是一道较简单的题目．

二、填空题

11．（2014年广东汕尾）4的平方根是　．

分析：根据平方根的定义，求数a的平方根，也就是求一个数x，使得x²=a，则x就是a的平方根，由此即可解决问题．

解：∵（±2）²=4，∴4的平方根是±2．故答案为：±2．

点评：本题考查了平方根的定义．注意一个正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根．