
4.在等差数列 中,
中,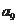 =
= ,则数列
,则数列 的前11项和
的前11项和 =( ).
=( ).
A.24 B.48 C.66 D.132
3.已知 ,如果
,如果 是
是 的充分不必要条件,则实数
的充分不必要条件,则实数 的取值范围是( )
的取值范围是( )
A.  B.
B.  C.
C.  D.
D. 
2.已知复数 ,则
,则 =(
)
=(
)
A.  B.
B.  C.
C.  D.
D. 
一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合 ,
, ,则( )
,则( )
A.A B
B.A
B
B.A B
C.A
B
C.A B
D.A
B
D.A B
B
23、本题满分11分。如图8,已知抛物线y= x2- x-3与x轴的交点为A、D(A在D的右侧),与y轴的交点为C。
(1)直接写出A、D、C三点的坐标;
(2)在抛物线的对称轴上找一点M,使得MD+MC的值最小,并求出点M的坐标;
(3)设点C关于抛物线对称的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,求出点P的坐标;若不存在,请说明理由。
解:(1)A(4,0) 、D(-2,0)、C(0,-3)
(2)连接AC,与抛物线的对称轴交点M即为所求,直线AC的解析式y=-3,
对称轴是直线x==1,把x=1代入y=-3得y=-
`∴M(1,-)
(3)如下图,当点P与D重合时,四边形ADCB是梯形,此时点P为(-2,0);
直线AB的解析式为y=,过点C作CP1//AB,与抛物线交于点P1,
直线CP1的解析式为y=,联立y= x2- x-3,可得P1(6,6)



22、本题满分10分。如图7,在Rt⊿ABC中,∠B=90°,AC=60,AB=30。点D是AC上的动点,过D作DF⊥BC于F,再过F作FE//AC,交AB于E。设CD=x,DF=y。
 (1)求y与x的函数关系式;
(1)求y与x的函数关系式;
(2)当四边形AEFD为菱形时,求x的值;
(3)当是⊿FED直角三角形时,求x的值。
解:(1)∵∠B=90°,AC=60,AB=30
∴∠C=30°
∴y=sin30°CD=
(2)当四边形AEFD为菱形时,有AD=DF
 ∴AC-CD=DF,即60-x=
∴AC-CD=DF,即60-x=
∴x=40
(3)当是⊿FED直角三角形时,只能是∠FDE=90°,如图6-2
由DF⊥BC得∠2=90°,即有DE//BC,所以四边形AEFD为平行四边形,显然AE=DF;
再由DE//BC可得:∠3=∠B=90°,∠4=∠C=30°
在Rt⊿BOC中,sin∠4==
∴AC-CD=2DF,即60-x= x
∴x=30
21、本题满分8分。如图6,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE。
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
(1)证明:
⇒⊿BCE≌⊿DCF⇒ CE=CF
(2)解:GE=BE+GD成立,理由是:7
⇒GE=BE+GD
20、本题满分8分。某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成。已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400 m2区域的绿化时,甲队比乙队少用4天。
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用是0.4万元,乙队为0.25万元,要使这次的绿化总费不超过8万元,至少应安排甲队工作多少天?
解:(1)设乙队每天绿化x m2,则:
解得:x=50,2x=100
答:甲、乙两工程队每天能完成绿化的面积分别是100、50m2。
(2)设至少应安排甲队工作y天,则:
 0.4y+×0.25≤8
0.4y+×0.25≤8
y≥10
19、本题满分8分。已知关于x的方程x2+ax+a-2=0。
(1)当该方程的一个根为1时,求a的值及该方程的另一根;
(2)求证:不论a取何实数,该方程都有两个不相等的实数根。
(1)解:设方程的另一根为x1;
解得:a=,x1=-
(2)证明:⊿=a2-4×(a-2)= (a-2)2+4
∵(a-2)2≥0
∴⊿>0
∴不论a取何实数,该方程都有两个不相等的实数根。
18、本题满分8分。如图5,在⊿ABO中,OA=OB,C是边AB的中点,以O为圆心的圆过点C。
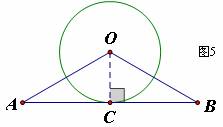 (1)求证:AB与⊙O相切;
(1)求证:AB与⊙O相切;
(2)若∠AOB=120°,AB=4,求⊙O的面积。
(1)证明:连接OC,
(2)∵C是边AB的中点,AB=4
∴BC=2
∵OA=OB,C是边AB的中点
∴中线OC可以表示高和∠AOB的平分线
∴在Rt⊿BOC中,∠BOC=60°,即有OC==2
S⊙O=4π
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com