
一、本大题共8小题,每小题5分,共40分。
1. 已知集合
已知集合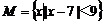 ,
,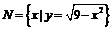 ,且
,且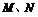 都是全集
都是全集 的子集,则下图韦恩图中阴影部分表示的集合( )
的子集,则下图韦恩图中阴影部分表示的集合( )
A.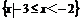 B.
B. C.
C. D.
D.
(二)选做题(14~15题,考生只能从中选做一题)
14. (坐标系与参数方程选做题)若以
(坐标系与参数方程选做题)若以 为极点,
为极点, 轴正半轴为极轴,曲线
轴正半轴为极轴,曲线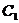 的极坐标方程为:
的极坐标方程为: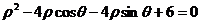 上的点到曲线
上的点到曲线 的参数方程为:
的参数方程为: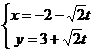 (
(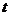 为参数)的距离的最小值为 .
为参数)的距离的最小值为 .
15.(几何证明选讲选做题)如图所示, 是半径等于
是半径等于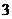 的圆
的圆 的直径,
的直径,
 是圆
是圆 的弦,
的弦, ,
, 的延长线交于点
的延长线交于点 ,若
,若 ,
, ,
,
则
二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分.
(一)必做题(9~13题)
9.函数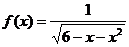 的定义域是________.
的定义域是________.
10. 已知向量
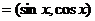 ,
,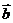
 ,且
,且 ∥
∥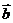 ,则
,则 ________
________
11. 已知两条平行直线 与
与 之间的距离是
之间的距离是
12. 抛物线 在
在 处的切线与
处的切线与 轴及该抛物线所围成的图形面积为
.
轴及该抛物线所围成的图形面积为
.
13.已知 ,若
,若 恒成立, 则
恒成立, 则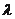 的取值范围是
的取值范围是
21、已知椭圆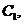
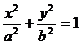 (a>b>0)抛物线
(a>b>0)抛物线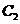
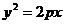 ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:
 |
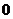 |
4 |
 |
1 |
 |
2 |
4 |
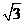 |
2 |
 (1)求
(1)求 的标准方程;
的标准方程;
(2)四边形ABCD的顶点在椭圆 上,且对角线AC、BD过原点O,若
上,且对角线AC、BD过原点O,若 ,
,
(i) 求 的最值.
的最值.
(ii) 求四边形ABCD的面积;
20、已知函数 满足
满足 ,当
,当 时,
时,
 ,当
,当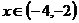 时,
时,  的最大值为-4.
的最大值为-4.
(I)求实数 的值;
的值;
(II)设 ,函数
,函数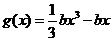 ,
, .若对任意的
.若对任意的 ,总存在
,总存在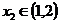 ,使
,使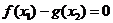 ,求实数
,求实数 的取值范围.
的取值范围.
19、已知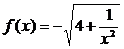 ,数列
,数列 的前n项和为
的前n项和为 ,点
,点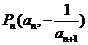 在曲线
在曲线 上
上 ,且
,且 ,
,
(1)求数列 的通项公式;
的通项公式;
(2)数列 的前n项和为
的前n项和为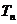 ,且满足
,且满足 ,
, ,求数列
,求数列 的通项公式;
的通项公式;
(3)求证: .
.
18、 如图,四棱锥
如图,四棱锥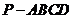 中,
中,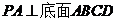 ,
,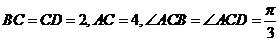 ,
,
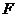 为
为 的中点,
的中点,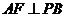 .
.
(1)求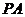 的长; (2)求二面角
的长; (2)求二面角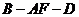 的正弦值.
的正弦值.
17、在一场娱乐晚会上, 有5位民间歌手(1至5号)登台演唱, 由现场数百名观众投票选出最受欢迎歌手. 各位观众须彼此独立地在选票上选3名歌手, 其中观众甲是1号歌手的歌迷, 他必选1号, 不选2号, 另在3至5号中随机选2名. 观众乙和丙对5位歌手的演唱没有偏爱, 因此在1至5号中随机选3名歌手.
(Ⅰ) 求观众甲选中3号歌手且观众乙未选中3号歌手的概率;
(Ⅱ) X表示3号歌手得到观众甲、乙、丙的票数之和, 求X的分布列和数学期望.
三、解答题
16、在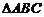 中,角
中,角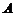 、
、 、
、 对的边分别为
对的边分别为 、
、 、
、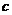 ,且
,且
(1)求 的值;
的值;
(2)若 ,求
,求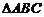 的面积
的面积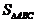 .
.
13、 14、 15、
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com