6．函数的值域为_________.

5．函数y=a^x在[0,1]上的最大值与最小值的和为3，则a的值为　　　 (　　 )

　 A. 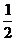　　　　　　B.　 2　　 　　　　　C. 4　　　　　　　 D.

4．设函数（且），且，则下列结论正确的是（　 　）

A．　　　　　　　 B．

C．　　　　　　　　　 D．

3．若函数是定义在R上的减函数，则实数a的取值范围是（　　 ）

A．a＜1　　　　　　　　　　　　 B．0＜a＜1

C．a＞1　　　　　　　　　　　　 D．a＞2

2．指数函数、、、在同一坐标系内的图象如图所示，则a、b、c、d的大小顺序是（　 ）

A．b＜a＜c＜d　　　　　 B．a＜b＜d＜c

C．b＜a＜d＜c　　　　　 D．b＜c＜a＜d

1．若函数、三、四象限，则（　　 ）

A．　　　　　 B．　

C． 　　 D．

5．指数函数的函数值与1的大小关系：

[典型例题]

[例1]比较下列各组题中各个值的大小：

（1）1.7^2.5 　与　 1.7³；　　　 （2）与；

（3）1.7^0.3 与 0.9^3.1；　　　 （4），，.

答案：（1）1.7^2.5 <1.7³；　　　 （2）<；

（3）1.7^0.3 >0.9^3.1；　　　 （4）>>.

[例2]求证：（1）是奇函数；

（2）是偶函数.

证明：（1）∵，∴f(x)是奇函数；

（2）∵，∴f(x)是偶函数.

[例3] 设0≤x≤2，求函数的最大值和最小值.

解：，设，则，

∵0≤x≤2，∴1≤t≤4，当t=3时，y有最小值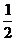；当t=1时，y有最大值.

[例4]（1）设函数为奇函数，求的值；

（2）已知且是R上的增函数，求的取值范围.

解：（1）对任意，有

（2）任取且.

则，

在上增函数，

又

当时，, 符合上述条件.

当时，，且即.

综上所述，的取值范围是

[强化训练]

4．在比较两数的大小时，若利用指数函数的单调性进行判断，一般先看是否为同底；若不能直接用函数单调性，需引入中间量（如与0，±1进行比较），综合运用函数的性质来解决．

3．指数函数既不是奇函数也不是偶函数，但底数互为倒数的两个指数函数的图象关于y轴对称．

2．指数函数的图象和性质：

	a＞1	0＜a＜1
图 　 　 　 象
性 　 质	（1）　　　 定义域是R； （2）　　　 值域是（0，+∞）； （3）　　　 图象过定点（0，1），即x=0时，y=1；
（4） 在R上是增函数	在R上是减函数