
4.下列命题:①若a·b=0,则a=0或b=0;②若a⊥b,则(a-b)2=a+b;③a·b= b·c,则a=c;④若a·b·c为非零向量,且a+b+c=0,则(a+b)·c<0其中正确命题个数为
A.1 B.2 C.3 D.4
3.设f(x)=x-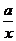 +a在(1,+∞)上为增函数,则实数a取值范围是
+a在(1,+∞)上为增函数,则实数a取值范围是
A.[0,+ ∞) B.[1,+ ∞) C.[-2,+ ∞) D.[-1,+ ∞)
2.已知复数z1=2+i,z2=1-i,则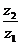 在复平面内对应的点位于
在复平面内对应的点位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,中有一个是符合题目要求的.
1.两个集合A与B之差记作“A/B”,定义A/B={x|x∈A,且x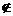 B|,如果集合A={x||x-2|≤1},B={x|log2x≥1,x∈R},那么A/B等于
B|,如果集合A={x||x-2|≤1},B={x|log2x≥1,x∈R},那么A/B等于
A.{x||x-2|≤1} B.{x|x<2,或x≥2} C.{x|x≤x<2} D.{x|0<x≤1}
22.(本题满分14分)
由坐标原点O向曲线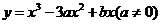 引切线,切于O以外的点
引切线,切于O以外的点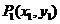 ,再由P1引此曲线的切线,切于P1以外的点
,再由P1引此曲线的切线,切于P1以外的点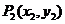 ,如此进行下去,得到点列
,如此进行下去,得到点列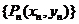 .
.
求:(Ⅰ)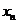 与
与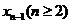 的关系式;
的关系式;
(Ⅱ)数列{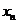 }的通项公式;
}的通项公式;
(Ⅲ)当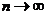 时,
时,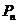 的极限位置的坐标.
的极限位置的坐标.
21.(本题满分12分)
已知在平面直角坐标系xoy中,向量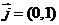 ,△OFP的面积为
,△OFP的面积为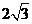 ,且
,且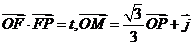 .
.
(Ⅰ)设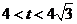 ,求向量
,求向量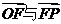 的夹角
的夹角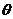 的取值范围;
的取值范围;
(Ⅱ)设以原点O为中心,对称轴在坐标轴上,以F为右焦点的椭圆经过点M,且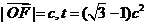 ,当
,当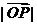 取最小值时,求椭圆的方程.
取最小值时,求椭圆的方程.



20.(本小题满分12分)
设函数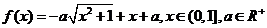 .
.
(Ⅰ)若f(x)在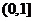 上是增函数,求a的取值范围;
上是增函数,求a的取值范围;
(Ⅱ)求f(x)在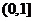 上的最大值.
上的最大值.
19.(本小题满分12分)
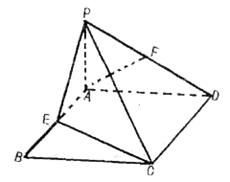
如图,PA⊥平面AC,四边形ABCD是矩形,E、F分别是AB、PD的中点.
(Ⅰ)求证:AF//平面PCE;
(Ⅱ)若二面角P—CD—B为45°AD=2,CD=3,求点F到平面PCE的距离.
高二班的一个研究性学习小组在网上查知,某珍惜植物种子在一定条件下发芽成功的概率为,该研究性学习小组又分成两个小组进行验证性实验.
(Ⅰ)第一小组做了5次这种植物种子的发芽实验(每次均种下一粒种子),求他们的实验至少有3次成功的概率;
(Ⅱ)第二小组做了若干次发芽实验(每次均种下一粒种子),如果在一次实验中种子发芽成功就停止实验,否则将继续进行下次实验,直到种子发芽成功为止,但发芽实验的次数最多不超过5次,求第二小组所做种子发芽实验的次数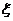 的概率分布列和期望.
的概率分布列和期望.
18.(本小题满分12分)


 已知O为坐标原点,
已知O为坐标原点,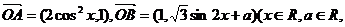 a是常数),若
a是常数),若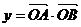 .
.
(Ⅰ)求y关于x的函数解析式f(x);
(Ⅱ)若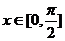 时,f(x)的最大值为2,求a的值并指出f(x)的单调区间.
时,f(x)的最大值为2,求a的值并指出f(x)的单调区间.
三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com