
二.填空题
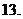 设
设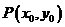 是函数
是函数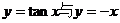 图象的交点,则
图象的交点,则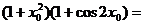 .
.
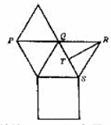
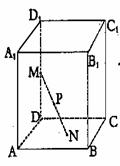
 如图是各棱长均相等的正四棱锥表面展开图,
如图是各棱长均相等的正四棱锥表面展开图,  为
为 的中点,则在四棱锥中
的中点,则在四棱锥中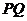 与
与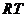 所成角的余弦值为____________.
所成角的余弦值为____________.
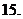 已知函数
已知函数 的定义域是
的定义域是 ,则实数
,则实数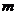 的取值范围是___________.
的取值范围是___________.
 从编号为
从编号为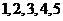 的五个球中任取
的五个球中任取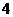 个,放在标号为
个,放在标号为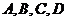 的四个盒子里,每盒一球,且
的四个盒子里,每盒一球,且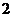 号球不能放在
号球不能放在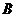 盒中,则不同的放法种数为____________(用数字作答)。
盒中,则不同的放法种数为____________(用数字作答)。
一.选择题:
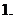 同时满足①
同时满足① 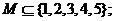 ② 若
② 若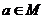 ,则
,则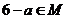 , 的非空集合
, 的非空集合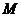 的个数有:
的个数有:
A.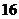 B.
B.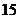 C.
C.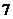 D.
D.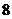
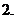 已知随机变量
已知随机变量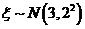 ,若
,若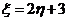 ,则
,则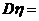
A.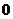 B.
B.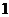 C.
C.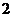 D.
D.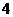
 设
设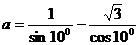 ,则
,则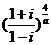 的值是:
的值是:
A.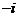 B.
B.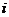 C.
C.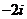 D.
D.
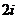
 定义在
定义在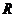 上的函数
上的函数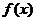 对任意
对任意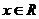 都有
都有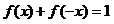 ,则
,则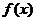 的图象必关于:
的图象必关于:
A.原点对称 B.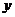 轴对称 C.点
轴对称 C.点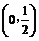 对称 D.点
对称 D.点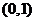 对称
对称
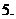 定义:称
定义:称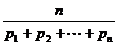 为
为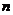 个正数
个正数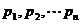 的“均倒数”,若数列{
的“均倒数”,若数列{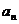 }的前
}的前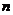 项的“均倒数”为
项的“均倒数”为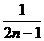 ,则数列{
,则数列{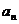 }的通项公式为:
}的通项公式为:
A.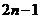 B.
B.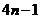 C.
C. 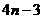 D.
D.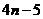
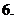 若
若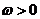 ,且函数
,且函数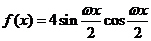 在
在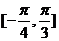 上单调递增,则
上单调递增,则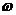 的取值范围是:
的取值范围是:
A. 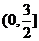 B.
B.
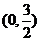 C.
C.
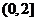 D.
D.
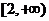
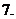 设
设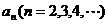 是
是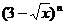 的展开式中
的展开式中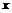 的一次项的系数,则
的一次项的系数,则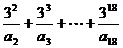 的值是:
的值是:
A.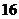 B.
B.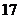 C.
C.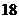 D.
D.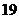
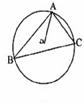
 已知点
已知点 为
为 的外心,且
的外心,且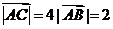 ,
,
则 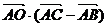 等于:
等于:
A.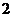 B.
B.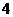
C.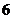 D.
D.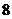
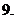 设曲线
设曲线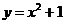 在其上任一点
在其上任一点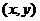 处的切线的斜率为
处的切线的斜率为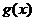 ,则函数
,则函数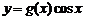 的部分图象可以为:
的部分图象可以为:

A. B. C. D.
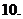 设
设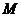 是
是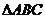 内一点,且
内一点,且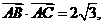
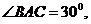 定义
定义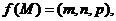 其中
其中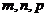 分别是
分别是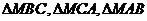 的面积,若
的面积,若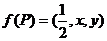 ,则
,则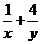 的最小值是:
的最小值是:
 A.
A. B.
B. C.
C.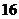 D.
D.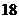
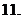 已知直平行六面体
已知直平行六面体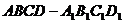 的各条棱长均为
的各条棱长均为 ,
,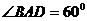
长为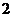 的线段
的线段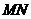 的一个端点
的一个端点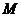 在
在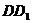 上运动, 另一个端点
上运动, 另一个端点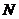 在底面
在底面
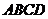 上运动,则
上运动,则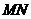 的中点
的中点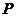 的轨迹(曲面)与共一顶点
的轨迹(曲面)与共一顶点 的三个面所
的三个面所
围成的几何体的体积为:
A.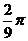 B.
B. 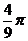 C.
C. 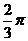 D.
D.
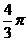
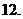 双曲线
双曲线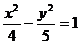 的左顶点为
的左顶点为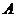 ,右焦点为
,右焦点为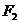 ,过
,过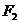 作
作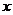 轴的垂线与双曲线的一个 交点为
轴的垂线与双曲线的一个 交点为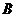 ,直线
,直线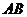 与双曲线的右准线交于点
与双曲线的右准线交于点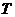 ,若
,若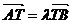 ,则
,则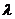 等于:
等于:
A. 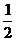 B.
B.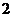 C.
C.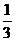 D.
D.


 第Ⅱ卷(非选择题部分共90分)
第Ⅱ卷(非选择题部分共90分)
22.(本小题满分14分)
数列{an}的首项a1=1,前n项和Sn满足2kSn-(2k+1)Sn-1=2k(常数k>0,n=2,3,4,…)
(1)求证:数列{an}是等比数列;
(2)设数列{an}的公比为f(k),作数列{bn},使b1=3,bn=f(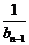 )(n=2,3,4,…)求数列{bn}的通项公式;
)(n=2,3,4,…)求数列{bn}的通项公式;
(3)设cn=bn-2,若存在m∈N*,使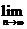 (cmcm+1+cm+1cm+2+…+cncn+1)<
(cmcm+1+cm+1cm+2+…+cncn+1)<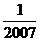 ,试求m的最小值.
,试求m的最小值.
21.(本小题满分12分)
已知函数f(x)=ax3+bx2+cx+d满足下列条件:
①过点(0,9);②方程f(-x)=f(x)的解为-3,0,3;③在x=-1处取得极大值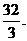
(1)求函数f(x)的解析式;
(2)讨论函数f(x)的单调性并求出单调区间;
(3)设函数f(x)在区间[t,t+1](t≤-1)上的最小值为g(t),求g(t)的解析式.
20.

 (本小题满分12分)
(本小题满分12分)
从6名男同学和4名女同学中随机选出3名同学参加一次测试,每个同学通过测试的概率为 0.7.求:
(1)选出的三位同学中至少有一名女同学的概率;
(2)同学甲被选中并且通过测试的概率;
(3)记选出的三位同学中女同学的个数为ξ,求ξ的分布列.
19.(本小题满分12分)
已知a=(sinθ,2tanθ),b=(1,sin2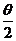 ),且a·b=3,求
),且a·b=3,求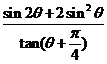 的值.
的值.
18.(本小题满分12分)
已知向量a,b满足|a|=|b|=1,且|a+kb|=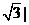 a-b|(k<0),
a-b|(k<0),
(1)试用k表示a·b,并求出a·b的最大值及此时a与b的夹角θ的值;
(2)当a·b取最大值时,求实数λ,使|λa-λb|的值最小.
三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
解不等式loga
16.设n为满足C1n+2C2n+3C3n+…+nCnn<450的最大自然数,则n=_____________.
15.在数列{an}中,a1=1,当n≥2时,an=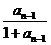 ,则
,则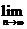 (a1a2+a2a3+…+anan+1)=_______.
(a1a2+a2a3+…+anan+1)=_______.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com