知识点精讲

1．函数的图象及其性质：

	a＞1	0＜a＜1
图 　 　 　 象
性 　 　 　 质	（1）定义域（0，+∞）； （2）值域R； （3）过点（1，0），即当x=1时，y=0；
（4）在（0，+∞）上是增函数	（4）在（0，+∞）上是减函数

图象特征	函数性质
（1）这些图象都在y轴右侧	（1）定义域是（0，+∞）
（2）函数图象都经过点（1，0）	（2）1的对数是零
（3）图象（Ⅰ）在（1，0）右边的纵坐标都大于0，在（1，0）点左边的纵坐标都小于0；图象（Ⅱ）正好相反．	（3）a＞1时，若x＞1，则logax＞0； 若0＜x＜1时，logax＜0； 0＜a＜1时，若x＞1，则logax＜0； 若0＜x＜1时，logax＞0；
（4）自左向右看，图象（Ⅰ）逐渐上升；图象（Ⅱ）逐渐下降．	（4）当底数a＞1时，是增函数；当底数0＜a＜1时，是减函数．

2.认识事物之间的相互转化；

教学重点：掌握对数函数的图象和性质．

教学难点：对数函数的定义，对数函数的图象和性质及应用．

3.掌握对数形式复合函数的单调性的判断及证明方法；

情感、态度、价值观：1.用联系的观点分析问题；

2.掌握同底对数、不同底对数的大小的比较方法；

4.同底数对数、不同底对数的大小的比较．

能力目标：1.理解对数函数的概念，掌握对数函数的图象和性质；

3.对数形式的复合函数的单调性；

教学知识点

知识目标：1.对数函数的概念、对数函数的单调性；

2.对数函数的图象和性质；

二．证明⒈直接证明

⑴综合法

一般地，利用已知条件和某些数学定义、定理、公理等，经过一系列的推理论证，最后推导出所要证明的结论成立，这种证明方法叫做综合法。综合法又叫顺推法或由因导果法。

⑵分析法

一般地，从要证明的结论出发，逐步寻求使它成立的充分条件，直至最后，把要证明的结论归结为判定一个明显成立的条件（已知条件、定义、定理、公理等），这种证明的方法叫分析法。分析法又叫逆推证法或执果索因法。

2．间接证明------反证法

一般地，假设原命题不成立，经过正确的推理，最后得出矛盾，因此说明假设错误，从而证明原命题成立，这种证明方法叫反证法。

第十五部分 推理与证明

1．推理：

⑴合情推理：归纳推理和类比推理都是根据已有事实，经过观察、分析、比较、联想，在进行归纳、类比，然后提出猜想的推理，我们把它们称为合情推理。

①归纳推理：由某类食物的部分对象具有某些特征，推出该类事物的全部对象都具有这些特征的推理，或者有个别事实概括出一般结论的推理，称为归纳推理，简称归纳。

注：归纳推理是由部分到整体，由个别到一般的推理。

②类比推理：由两类对象具有类似和其中一类对象的某些已知特征，推出另一类对象也具有这些特征的推理，称为类比推理，简称类比。

注：类比推理是特殊到特殊的推理。

⑵演绎推理：从一般的原理出发，推出某个特殊情况下的结论，这种推理叫演绎推理。

注：演绎推理是由一般到特殊的推理。

“三段论”是演绎推理的一般模式，包括：⑴大前提---------已知的一般结论；⑵小前提---------所研究的特殊情况；⑶结　 论---------根据一般原理，对特殊情况得出的判断。

4．全称量词与存在量词

⑴全称量词-------“所有的”、“任意一个”等，用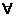表示；

　 全称命题p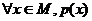：； 全称命题p的否定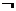p：。

⑵存在量词--------“存在一个”、“至少有一个”等，用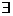表示；

　 特称命题p：； 特称命题p的否定p：；