
5.已知全集I=R,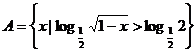 ,则
,则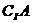 = (
) A.
= (
) A.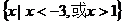 B.
B.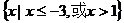
C.  D.
D. 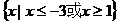
[同步训练高级]
4.比较下列各组数的大小关系:
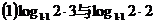 ;
;
 .
.
3.将log0。70.8,log1.10.9,1.10。9按照从小到大的顺序排列.
2.已知函数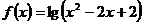 的定义域为F,函数
的定义域为F,函数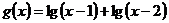 的定义域为G,那么
( ) A.
的定义域为G,那么
( ) A.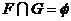 B. F=G
C. F
B. F=G
C. F
 G D.F
G D.F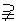 G
G
1.四个函数分别为① ;②
;②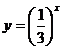 ;③
;③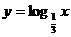 ;④
;④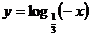 . 其图象关于原点对称的是
(
)
. 其图象关于原点对称的是
(
)
A.②和③ B.①和② C.②和④ D.①和②、③和④
2.对于logab的正负性,可直接利用下列性质来判断:
(1) 若a>1,b>1,或0<a<1,0<b<1时,logab>0;
(2) 若a>1,0<b<1或b>1,0<a<1时,logab<0.
[例3]证明函数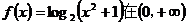 上是增函数;并判断
上是增函数;并判断
上是增函数还是减函数?
分析:此题目的是在于让学生熟悉函数单调性证明的通法,同时熟悉利用对数函数的单调性比较同底数对数大小的方法.
证明: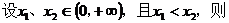
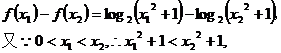
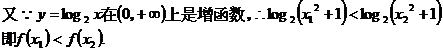
∴函数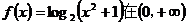 上是增函数;
上是增函数;
同理可证函数 上是减函数.
上是减函数.
[自我检测]
[同步训练初级]
1.当比较的对数值是底数相同的情况时,只需考虑相应对数函数的单调性,利用函数的单调性来判断大小;当比较的数值是底数不相同的情况时,常常需要引入中间值(例如0或1)来间接比较它们的大小;
4.和指数函数的单调性一样,当a>1时,y=logax在(0,+∞)上是增函数,当0<a<1时,y=logax在(0,+∞)上是减函数.
[应用举例]
[例 1]求下列函数的定义域:
(1) y=logax2; (2)y=loga(4-x); (3)y=loga(9-x2);
(4)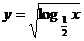 ;
; 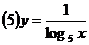 .
.
解:(1)∵x2>0,∴x≠0,∴定义域是{x|x∈R且x≠0};
(2)∵4-x>0,∴x<4,∴定义域是{x|x<4};
(3)∵9-x2>0,∴-3<x<3,∴定义域是{x|-3<x<3};
(4)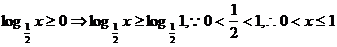 ,∴定义域是{x|0<x≤1};
,∴定义域是{x|0<x≤1};
(5)∵log5x≠0,∴log5x≠log51,∴x≠1,∴定义域为{x|x≠1}.
求函数定义域方法小结:
(1) 分母不能为零;
(2) 偶次方根的被开方数大于或等于零;
(3) 对数的真数必须大于零;
(4) 指数函数、对数函数的底数要求大于零且不等于1.
[例 2]比较下列各组数中两个值的大小:
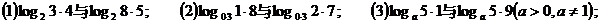
(4)log76,log67 ; (5)log3p,log20.8.
解:(1)考察对数函数y=log2x,
∵2>1,∴y=log2x在(0,+∞)上是增函数,
∴log23.4<log28.5.
(2)考察对数函数y=log0.3x,
∵0.3<1,∴y=log0.3x在(0,+∞)上是减函数,
∴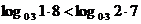 .
.
(3)由于两个对数的底数a大小不一定,而a的大小直接影响函数的单调性,因此要对底数进行讨论:
当a>1时,y=logax在(0,+∞)上是增函数,∴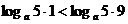 ;
;
当0<a<1时,y=logax在(0,+∞)上是减函数,∴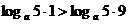 .
.
(4)∵log76>log66=1,log67<log77=1,∴log76>log67.
(5)∵log3p>log31=0,log20.8<log21=0,∴log3p>log20.8.
小结:
3.(1,0)为所有对数函数图象的交汇点;
2.对数函数的定义域、值域分别为相应的指数函数的值域和定义域,它们的图象关于直线y=x对称;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com