二、选择题

15.　　 　已知为异面直线,平面,平面.平面α与β外的直线满足,则（D　）

A．,且　　　　　　　　　 B．,且

C．与相交,且交线垂直于　　　　 D．与相交,且交线平行于

14.　　 一个半径为1的小球在一个内壁棱长为的正四面体封闭容器内可向各个方向自由运动，则该小球表面永远不可能接触到的容器内壁的面积是　　 　　　．　　　　　　　　　　　 　　　

[解] 如答12图1，考虑小球挤在一个角时的情况，记小球半径为，作平面//平面，与小球相切于点，则小球球心为正四面体的中心，，垂足为的中心．

因

，

故，从而．

记此时小球与面的切点为，连接，则

．

考虑小球与正四面体的一个面(不妨取为)相切时的情况，易知小球在面上最靠近边的切点的轨迹仍为正三角形，记为，如答12图2．记正四面体

的棱长为，过作于．

　 因，有，故小三角形的边长．

小球与面不能接触到的部分的面积为（如答12图2中阴影部分）

．　　　　　

又，，所以

．

由对称性，且正四面体共4个面，所以小球不能接触到的容器内壁的面积共为．

13.　　 在直三棱柱中，底面ABC为直角三角形，，. 已知Ｇ与Ｅ分别为和的中点，Ｄ与Ｆ分别为线段和上的动点（不包括端点）. 若，则线段的长度的最小值为　　 　　　　　　。

[解]建立直角坐标系，以Ａ为坐标原点，ＡＢ为ｘ轴，ＡＣ为ｙ轴，ＡＡ_１为ｚ轴，则（），，，（）。所以，。因为，所以，由此推出 。又，，从而有 。

12.　　 如图是一个正方体的表面展开图，A、B、C均为棱的中点，D是顶点，

　　 则在正方体中，异面直线AB和CD的夹角的余弦值为　　 　　　　　。

11.　　 设复数，，在复平面上所对应点在

　　 直线上，则=　　　 　　。

10.　　 用0、1、2、3、4、5组成一个无重复数字的五位数，这个数是偶数的概率为　 　　。

9.　　　　 从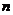个正整数中任意取出两个不同的数,若取出的两数之和等于的概率为,则　8 。

8.　　　　 用4种颜色给一个正四面体的4个顶点染色，若同一条棱的两个端点不能用相同的颜色，那么不同的染色方法共有_____24________种。　

7.　　　　 将三个1、三个2、三个3填入3×3的方格中，要求每行、每列都没有重复数字，则不同的填写方法共有　 12　　　 种。

6.　　　 8名同学争夺3项冠军，获得冠军的可能性有　　 512　　　 种。