
4.对于定义在R上的函数 ,有下述命题:
,有下述命题:
 ①若
①若 是奇函数,则
是奇函数,则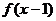 的图像关于点A(1,0)对称;
的图像关于点A(1,0)对称;
②若函数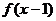 的图像关于直线
的图像关于直线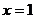 对称,则
对称,则 为偶函数;
为偶函数;
③若对 ,有
,有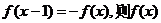 的周期为2;
的周期为2;
④函数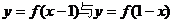 的图像关于直线
的图像关于直线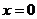 对称.
对称.
其中正确命题的序号是 ① ② ③
3. 定义在
定义在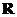 上的函数
上的函数 满足
满足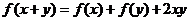 (
(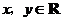 ),
),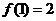 ,则
,则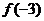 =__________ 6.
=__________ 6.
2.记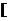
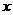
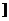 表示不超过
表示不超过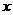 的最大整数,则函数
的最大整数,则函数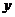 =
=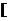

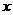
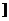 的图像与函数
的图像与函数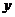 =
=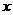 -1的图像的交点个数为
.0
-1的图像的交点个数为
.0
1. 已知: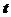 为常数,函数
为常数,函数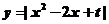 在区间
在区间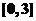 上的最大值为
上的最大值为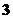 ,则实数
,则实数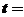 _____. 0或-2
_____. 0或-2
26、如图,直线l1∥l2,P在直线AB上.
(1)当点P在如图所示的位置时,试找出∠PCA,∠PDB,∠CPD之间的数量关系并说明理由;
(2)当点P在AB两点之间运动时,∠PCA,∠PDB,∠CPD之间的数量关是否发生变化;
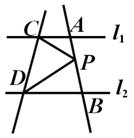 (3)当点P在直线AB上(不在线段AB上)运动时,试探究∠PCA,∠PDB,∠CPD之间的数量关系(只要写出结论)
(3)当点P在直线AB上(不在线段AB上)运动时,试探究∠PCA,∠PDB,∠CPD之间的数量关系(只要写出结论)
25、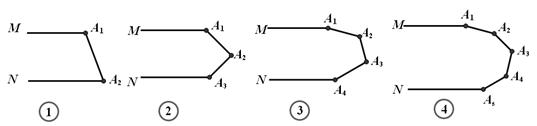 仔细观察,寻找规律:在图中的各图的MA1与NAn平行。
仔细观察,寻找规律:在图中的各图的MA1与NAn平行。
……
(1)图①中的∠A1+∠A2= 度;
图②中的∠A1+∠A2+∠A3= 度;
图③中的∠A1+∠A2+∠A3+∠A4= 度;
图④中的∠A1+∠A2 +∠A3+∠A4+∠A5= 度;
…………………………
第⑩个图中的∠A1+∠A2 +∠A3+……+∠A11= 度;
(2)按上图规律,第n个图中的
∠A1+∠A2 +∠A3+……+∠An+1= 度。
24、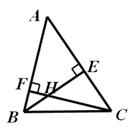 如图,在△ABC中,∠ABC=66°,∠ACB=54°,BE是AC上的高,CF是AB上的高,求∠ABE,
如图,在△ABC中,∠ABC=66°,∠ACB=54°,BE是AC上的高,CF是AB上的高,求∠ABE,
∠ACF和∠BHC的度数。
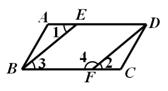
23、如图,AD∥BC,∠1=∠2.求证:∠3+∠4=180°.
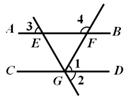
22、如图,∠1=∠2=∠3=60°,求∠4的度数.
21、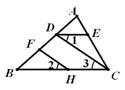 如图,已知HF∥CD,∠1=∠2,∠CED=100°,求∠ACB的度数.
如图,已知HF∥CD,∠1=∠2,∠CED=100°,求∠ACB的度数.
解:∵HF∥CD,∴∠2= .( )
又∵∠1=∠2,∴∠1=∠3.(等量代换)
∴DE∥ .( )
∴∠CED+ =180°.( )
又∵∠CED=100°,∴∠ACB= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com