
23(1)选择反比例函数,设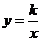 ,得
,得
k=12000
∴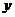 关于
关于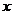 的函数关系式是
的函数关系式是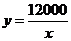 ………………………………2分
………………………………2分
不选另外一个函数的理由:
点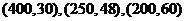 不在同一直线上,所以
不在同一直线上,所以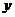 不是
不是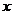 的一次函数. ………… 3分
的一次函数. ………… 3分
(2)第四天的销售量为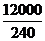 =50千克………………………………4分
=50千克………………………………4分
2 104-(30+40+48+50+60+80+96+100)=1 600,
即8天试销后,余下的海产品还有1 600千克.………………………………5分
当x=150时,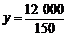 =80. ……………………………………6分
=80. ……………………………………6分
1 600÷80=20,所以余下的这些海产品预计再用20天可以全部售出 ……7分
(3)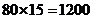 1600-1200=400……………………………………8分
1600-1200=400……………………………………8分
设新确定的价格为每千克x元。
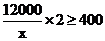
解得: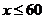 ……………………………………9分
……………………………………9分
答:新确定的价格最高不超过每千克60元才能完成销售任务…………………………10分
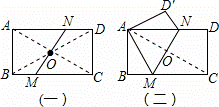 24解答:(1)证明:如图(一),连AC、BD交于O,
∵AD∥BC,
∴∠DNM=∠BMN,
∵四边形ABCD是矩形,
∴AB=CD,
∵∠BOM=∠DON,
∴△DON≌△BOM,
∴ND=BM,
同理可证△AON≌△COM,
∴AN=MC,
∴AN+ND=BM+MC,
∵AB=CD,
∴S梯形ABMN=S梯形CDNM;……………………………………4分
(2)解:如图(二),
∵AB=CD=AD′,
∵∠BAM+∠MAN=90°,∠MAN+∠NAD′=90°,
∴∠BAM=∠NAD′,又∠B=∠D′=90°,
∴△ABM≌△AD′N……………………………………………………6分
∴△ABM和△AD′N的面积相等,MC=AM=AN,
∵重叠部分是△AMN,不重叠部分是△ABM和△AD′N.
∴
24解答:(1)证明:如图(一),连AC、BD交于O,
∵AD∥BC,
∴∠DNM=∠BMN,
∵四边形ABCD是矩形,
∴AB=CD,
∵∠BOM=∠DON,
∴△DON≌△BOM,
∴ND=BM,
同理可证△AON≌△COM,
∴AN=MC,
∴AN+ND=BM+MC,
∵AB=CD,
∴S梯形ABMN=S梯形CDNM;……………………………………4分
(2)解:如图(二),
∵AB=CD=AD′,
∵∠BAM+∠MAN=90°,∠MAN+∠NAD′=90°,
∴∠BAM=∠NAD′,又∠B=∠D′=90°,
∴△ABM≌△AD′N……………………………………………………6分
∴△ABM和△AD′N的面积相等,MC=AM=AN,
∵重叠部分是△AMN,不重叠部分是△ABM和△AD′N.
∴ ,即
,即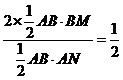
故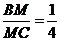 …………………………………………………………8分
…………………………………………………………8分
(3)MN⊥AC …………………………………………………………10分
22(1)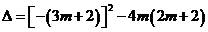 …………………………………1分
…………………………………1分
=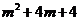
=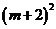 …………………………………2分
…………………………………2分
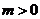
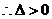
则原方程有两个不相等的实数根…………………………………3分
(2)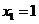 ,
,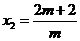 …………………………………5分
…………………………………5分
函数解析式为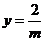 …………………………………6分
…………………………………6分
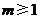 …………………………………8分
…………………………………8分
25(本小题满分12分)
如图1,△ABC,△AED都是等腰直角三角形,∠ABC=∠E=90°,AE=a,AB=b,且(a<b),点D在AC上,连接BD,BD=c.
(1) 如果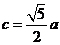 ,①求
,①求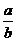 的值
的值
②若a,b是关于x的方程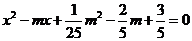 的两根,求m
的两根,求m
(2)如图2,将△ADE绕点A逆时针旋转,使BE=100,连接DC,求五边形ABCDE的面积
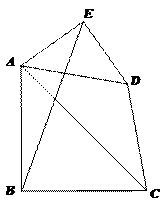
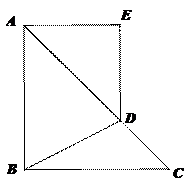
|
|
2013九年级起点考试
数学试卷评分细则
一选择题(每小题3分)
1 D 2 D 3 C 4 D 5 D 6 A 7 A 8 A 9 A 10 D
二填空题
11 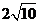 ,
,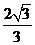 ,
, 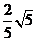 12 145.5
13
12 145.5
13 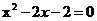
14 1.24
15 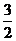 16
16 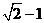
三解答题
17 原式= 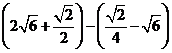 …………………………………3分
…………………………………3分
=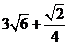 …………………………………6分
…………………………………6分
18 解 a=1 b=-8 c=17 …………………………………3分
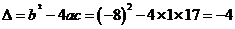 …………………………………5分
…………………………………5分
原方程无实数根…………………………………6分
19连接BD,交AC于点O
四边形ABCD是平行四边形
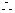 AO=CO,BO=DO…………………………………2分
AO=CO,BO=DO…………………………………2分
AE=CF
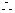 EO=FO…………………………………4分
EO=FO…………………………………4分
又BO=DO
 四边形BFDE是平行四边形…………………………………6分
四边形BFDE是平行四边形…………………………………6分
20 解设每轮传染中平均一个人传染了x个人
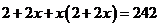 …………………………………3分
…………………………………3分
解得: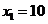
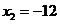 …………………………………5分
…………………………………5分
答:每轮传染中平均一个人传染了10个人…………………………………6分
21(1) 2分
(2)2分 (3)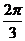 3分
3分
24(本小题满分10分)
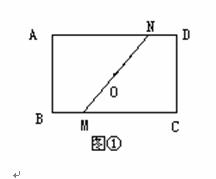
已知在矩形ABCD中,AD>AB,O为对角线的交点,过O作一直线分别交BC、AD于M、N。
(1)如图①,求证:梯形ABMN的面积等于梯形CDNM的面积
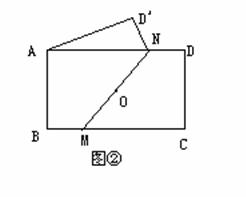
(2)如图②,若矩形ABCD沿MN折叠,能使得点C与点A重合,且翻折后不重叠部分的面积是重叠部分的面积的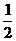 ,求BM:MC的值。
,求BM:MC的值。
(3)矩形ABCD沿MN折叠,当MN满足 时,才能使得点C恰好与点A重合(只写出的,不要求证明);
23(本小题满分10分)水产公司有一种海产品共2104千克,为寻求合适的销售价格,进行了8天试销,试销情况如下:
|
|
第1天 |
第2天 |
第3天 |
第4天 |
第5天 |
第6天 |
第7天 |
第8天 |
|
售价
x(元/千克) |
400 |
|
250 |
240 |
200 |
150 |
125 |
120 |
|
销售量
y(千克) |
30 |
40 |
48 |
|
60 |
80 |
96 |
100 |
观察表中数据,发现这种海产品的每天销售量y(千克)是销售价格x(元/千克)的函数.且这种函数是反比例函数、一次函数中的一种.  (1)请你选择一种合适的函数,求出它的函数关系式,并简要说明不选择另外一种函数的理由;
(1)请你选择一种合适的函数,求出它的函数关系式,并简要说明不选择另外一种函数的理由;
(2)在试销8天后,公司决定将这种海产品的销售价格定为150元/千克,并且每天都按这个价格销售,那么余下的这些海产品预计再用多少天可以全部售出? (3)在按(2)中定价继续销售15天后,公司发现剩余的这些海产品必须在不超过2天内全部售出,此时需要重新确定一个销售价格,使后面两天都按新的价格销售,那么新确定的价格最高不超过每千克多少元才能完成销售任务?
22(本小题满分8分)已知关于x的一元二次方程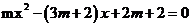 ,(m>0).
,(m>0).
(1)求证:方程有两个不相等的实数根
(2)设方程的两个实数根分别为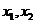 (其中
(其中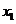 <
<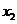 ),若y是关于m的函数,且
),若y是关于m的函数,且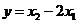 ,
,
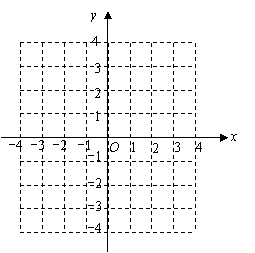 结合函数的图象回答,当自变量
结合函数的图象回答,当自变量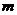 的取值范围满足满足什么条件时,
的取值范围满足满足什么条件时,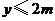 .
.
21(本小题满分7分)在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(2,3),
B(2,1),C(3,2)
 (1)画出△ABC
(1)画出△ABC
(2)画出△ABC 关于x轴对称的△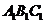
(3)如果将△ABC沿着边AB旋转,则所得
旋转体的体积为
20(本小题满分6分)有两人患了流感,经过两轮传染后共有242人患了流感,每轮传染中平均一个人传染了几个人?
19(本小题满分6分)已知□ABCD的对角线AC,点E,F是AC上的两点,并且AE=CF,求证:四边形BFDE是平行四边形

18(本小题满分6分)解一元二次方程: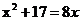
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com