
5.有9位同学参加歌咏比赛,所得的分数互不相同,取得分前5位同学进入决赛. 某同学知道自己的分数后,要判断自己能否进入决赛,他只需知道这9位同学的
A.平均数 B.众数 C.中位数 D.方差
4.下列运算正确的是
A.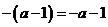 B.
B. C.
C.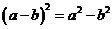 D.
D.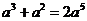
3.函数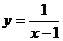 中,自变量x的取值范围是
中,自变量x的取值范围是
A. x <1 B. x = 1 C.x > 1 D.x 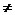 1
1
2.2013年我市各类全日制学校在校学生172.70万人,该数据用科学记数法表示为
A.1.727×106 人 B.1.727×105 人 C.1.727×104 人 D.1.727×103人
一、选择题
1.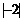 的值是 A.-2
B.2
C.
的值是 A.-2
B.2
C.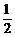 D.-
D.-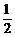
七. 解:由已知得,2和3是相应方程kx2-2x+6k<0的两根且k>0,即得k=.
……4分
(2)令f(x)= kx2-2x+6k,原问题等价于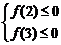
解得k≤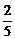 ,又k>0
,又k>0
∴实数k的取值范围是(0,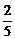 ]. ……4分
]. ……4分
(3)对应方程的Δ=4-24k2,令f(x)= kx2-2x+6k,
则原问题等价于Δ≤0或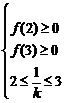
由Δ≤0解得k≤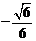 或k≥
或k≥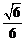 ,又k>0,∴k≥
,又k>0,∴k≥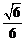 ……2分
……2分
由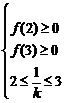 解得
解得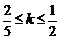 ……3分
……3分
综上,符合条件的k的取值范围是[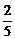 ,+∞) ……1分
,+∞) ……1分
六. 解:标价为1000元的商品消费金额为800元,获得奖券130元,优惠额为
330元,所以优惠率为0.33. ……4分
(2)y=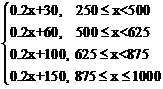 ……4分
……4分
(3)购买标价在[625,800)(元)内的商品,消费金额在[500,640)(元)内。
设顾客购买标价为x元的商品,(625≤x<800),消费金额为0.8x.获得奖券
100元,此时优惠率为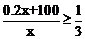 ,解得x≤750
,解得x≤750
综上所述,顾客购买标价的取值范围为[625,750](元)时,可得到不小于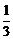 的
的
优惠率。 ……4分
五. 解:若 a1、a2、…、an∈R,a1+a2+…+an=1,
求证:a12+a22+…+an2≥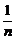 。 ……4分
。 ……4分
(2)证明:构造函数f(x)=(x-a1)2+(x-a2)2+…+ (x-an)2,
f(x)=nx2-2(a1+a2+…+an)x+a12+a22+…+an2
因为对一切x∈R,恒有f(x)≥0成立,所以Δ=4-4n(a12+a22+…+an2)≤0,
从而证得a12+a22+…+an2≥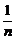 . ……6分
. ……6分
四. 解:a=0时,原不等式即为-x+1<0,∴原不等式解集为;…2分
(2)a≠0时,不等式对应方程的两根为1和 。
。
当0<a<1时, >1,原不等式解集为(1,
>1,原不等式解集为(1,  );……2分
);……2分
当a=1时, =1,,原不等式解集为Ф; ……2分
=1,,原不等式解集为Ф; ……2分
当a>1时, <1原不等式解集为(
<1原不等式解集为( ,1) ……2分
,1) ……2分
三. 解:A=[a-1,a+1] ……3分
B=(-∞,1)∪(4,+∞) ……3分
∵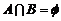 ,∴ a-1≥1且a+1≤4, ∴ a∈[2,3] ……2分
,∴ a-1≥1且a+1≤4, ∴ a∈[2,3] ……2分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com