
28、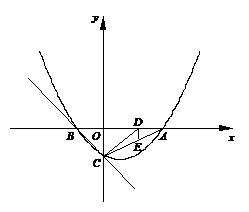 如图,已知抛物线
如图,已知抛物线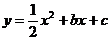 与y轴相交于点C,与x轴相交于A、B两点,点A的坐标为(2,0),点C的坐标为(0,-1).
与y轴相交于点C,与x轴相交于A、B两点,点A的坐标为(2,0),点C的坐标为(0,-1).
(1)求抛物线的函数关系式;
(2)点E是线段AC上一动点(与点A、C不重合),过点E作DE⊥x
轴于点D,连结DC,当△DCE的面积最大时,求点D的坐标;
(3)在直线BC上是否存在一点P(与点C不重合),使△ACP为等腰
三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.
27、(本题8分)已知,△ABC为等边三角形,点D为直线BC上一动点(点D不与B、C重合).以AD为边作菱形ADEF,使∠DAF=60°,连接CF.
⑴如图1,当点D在边BC上时,
①求证:∠ADB=∠AFC;②请直接判断结论∠AFC=∠ACB+∠DAC是否成立;
⑵如图2,当点D在边BC的延长线上时,其他条件不变,结论∠AFC=∠ACB+∠DAC是否成立?请写出∠AFC、∠ACB、∠DAC之间存在的数量关系,并写出证明过程;
⑶如图3,当点D在边CB的延长线上时,且点A、F分别在直线BC的异侧,其他条件不变,请补全图形,并直接写出∠AFC、∠ACB、∠DAC之间存在的等量关系.


26、(本题8分)周末,小明骑自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.
 (1)求小明骑车的速度和在甲地游玩的时间;
(1)求小明骑车的速度和在甲地游玩的时间;
(2)小明从家出发多少小时后被妈妈追上?此时离家多远?
(3)若妈妈比小明早10分钟到达乙地,求从家到乙地的路程.
25、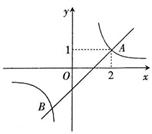 (本题6分)如图,一次函数
(本题6分)如图,一次函数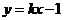 的图象与反比例函数
的图象与反比例函数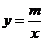 的图象交于A、B两点,其中A点坐标为(2,1).
的图象交于A、B两点,其中A点坐标为(2,1).
⑴试确定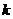 、
、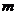 的值;
的值;
⑵求B点的坐标.
24、(本题6分)如图,PA与⊙O相切于A点,弦AB⊥OP,垂足为C,OP与⊙O相交于D点,已知OA=2,
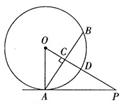 OP=4.
OP=4.
⑴求∠POA的度数;
⑵计算弦AB的长.
23、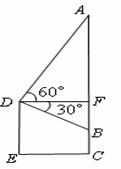 (本题6分)如图是使用测角仪测量一幅壁画高度的示意图.已知壁画AB的底端距离地面的高度BC=1m,在壁画的正前方点D处测得壁画顶端的仰角∠ADF=60°,底端的俯角∠BDF=30°,且点D距离地面的高度DE=2m,求壁画AB的高度.
(本题6分)如图是使用测角仪测量一幅壁画高度的示意图.已知壁画AB的底端距离地面的高度BC=1m,在壁画的正前方点D处测得壁画顶端的仰角∠ADF=60°,底端的俯角∠BDF=30°,且点D距离地面的高度DE=2m,求壁画AB的高度.
22、(本题6分)在□ABCD中,E、F分别是AB、CD的中点,连接AF、CE.
(1)求证:△BEC ≌△DFA;
(2)连接AC,当CA=CB时,判断四边形AECF是什么特殊四边形?并证明你的结论.
21、(本题5分)一个口袋中有4个相同的小球,分别与写有字母A、B、C、D,随机地抽出一个小球后放回,再随机地抽出一个小球.
(1)使用列表法或树形法中的一种,列举出两次抽出的球上字母的所有可能结果;
(2)求两次抽出的球上字母相同的概率.
20、(本题6分)某校组织了八年级800名学生参加的旅游地理知识竞赛,李老师为了了解学生对旅游地理知识的掌握情况,从中随机抽取了部分学生的成绩作为样本,把成绩按优秀、良好、及格和不及格4个级别进行统计,并绘制了如图所示的条形统计图和扇形统计图(部分信息未给出).
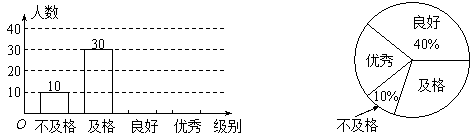
请根据以上提供的信息,解答下列问题:
(1)求被抽取部分学生的人数;
(2)请补全条形统计图,并求出扇形统计图中表示及格的扇形的圆心角度数;
(3)请估计八年级800名学生中达到良好和优秀的总人数.
17、如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7……叫做“正六边形的渐开线”,其中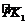 ,
,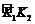 ,
,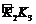 ,
,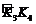 ,
,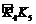 ,
,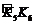 ,……的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为l1,l2,l3,l4,l5,l6,…….当AB=1时,l2 011等于( )
,……的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为l1,l2,l3,l4,l5,l6,…….当AB=1时,l2 011等于( )
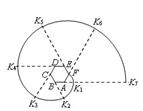 A、
A、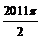 B、
B、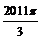 C、
C、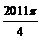 D、
D、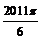
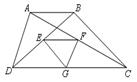
第16题 第17题
三、解答题(本大题共11小题,满分81分)
18、(本题满分8分)
(1)计算: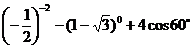 (2)化简:
(2)化简: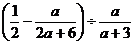
19、(本题满分10分)
(1)解方程: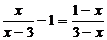 (2)解不等式组:
(2)解不等式组: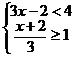
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com