3.〈江苏扬州〉将抛物线y=x²+1先向左平移2个单位，再向下平移3 个单位，那么所得抛物线对应的函数关系式是（　　 ）

A.y（x+2）²+2　　　　　 　B.y=（x+2）²-2

C.y=（x-2）²+2　　　　 　　D.y=（x-2）²-2

2.〈四川资阳〉在一个不透明的盒子里，装有4个黑球和若干个白球，它们除颜色外没有任何其他区别，摇匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复，共摸球40次，其中10次摸到黑球，则估计盒子中有白球（　　 ）

A.12个　　　 B.16个　　　 C.20个　　　 D.30个

一、选择题

1.〈山东枣庄〉如图1，该图形绕点O按下列角度旋转后，不能与其自身重合的是（　　 ）

　　　　　 　　　　　　　　　图1

A.72°　　　 B.108°　　　 C.144°　　　 D.216°

25．(12分)如图，线段AL上有一点B，且AL=15cm， AB=3cm．点M从点A出发，以1cm/s的速度沿线段AL向终点L匀速运动；与此同时，点N从点B出发，以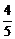cm/s的速度沿线段BL向终点L匀速运动．以AM为一边在线段AL的上方作矩形AMCD，使AD=4cm；以BN为斜边在AL的上方作等腰Rt△BNE．设运动时间为t（s）．

（1）求两点B、M重合时t的值．

（2）求t=5时BM的长度．

（3）当矩形AMCD与△BNE有重叠部分时，求重叠（阴影）部分图形的面积S（单位：cm²）与t的函数关系式．

（4）当矩形AMCD的边与等腰Rt△BNE相交时，沿矩形AMCD的边把△BNE剪开，用得到的图形拼成不重叠且无缝隙的图形恰好是梯形．请直接写出所有符合上述条件的t值．

24．（10分） 甲、乙两名同学住在同一栋楼，在同一所中学读书，沿同一条路上学且途中要经过一个书报亭．某日，乙比甲早一点出发步行上学，甲骑自行车上学．下图表示甲、乙两人到书报亭的路程y_­甲、y­­­_乙（单位：米）与甲出发时间x（分）的函数图象，根据图象信息解答下列问题：

（1）两同学的家到书报亭的路程是______米，家到学校的路程是______米．

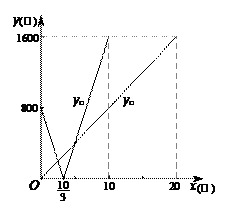（2）求乙的速度及乙比甲早出发的时间．

（3）求y_­甲与x的函数关系式．

　（4）求甲乙两名同学到书报亭的路程相等时刻的时间．

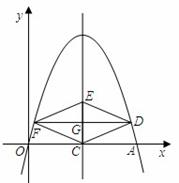
23.(8分) （1）操作发现：如图①，在矩形ABCD中，E是BC的中点，将△ABE沿AE折叠后得到△AFE，点F在矩形ABCD内部，延长AF交CD于点G，连FC，猜想△GFC的形状，并证明你的结论。

（2）。类比探究：如图②，将（1）中的矩形ABCD改为平行四边形，其它条件不变，（1）中的结论是否仍然成立？请说明理由。

　　　　　 图①　　　　　　　　　　　　　　 图②

22．（8分）如图，在平面直角坐标系中，抛物线经过点A（4，0）.直线x=2与x轴交于点C， 点E是直线x=2上的一个动点，过线段CE的中点G作DF⊥CE交抛物线于D、F两点.

（1）求这条抛物线的解析式.

（2）当点E落在抛物线顶点上时，求DF的长.

（3）当四边形CDEF是正方形时，求点E的坐标.

21．（7分）如图，矩形ABCO（OAOC）的两边分别在x轴的负半轴和y轴的正半轴上，点B在反比例函数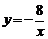（x<0）的图象上，且OC=2．将矩形ABCO以C为旋转中心，逆时针旋转90°后得到矩形EFCD，反比例函数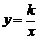（x<0）的图象经过点E．

　 （1）求 k的值．

　 （2）判断线段BE的中点M是否在反比例函数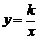（x<0）的图象上，请说明理由．

20．（6分）市积极开展“阳光体育大课间”活动，各校学生坚持每天锻炼一小时，某校根据实际，决定主要开设羽毛球、跳绳、踢毽子，三种运动项目．为了解学生最喜欢参加哪一种项目，随机抽取了n名学生进行调查（每名同学选择一种体育项目），并将调查结果绘制成如下两个统计图．

请结合上述信息解答下列问题：

（1）求n的值．

（2）请把条形统计图补充完整．

（3）已知该校有1 200人，请你根据统计图中的资料估计全校最喜欢踢毽子的人数．

19．(6分)某环卫清洁队承担着9600米长的街道清雪任务．在清雪1600米后，为了减少对交通的影响，决定租用清雪机清雪，结果共用了4小时就完成了清雪任务．已知使用清雪机后的工作效率是原来的5倍，求原来每小时清雪多少米？