
14.4 点拨:本题考查相似三角形的判定和性质,易忽略隐含条件树和地面垂直,而判断不出三角形相似,从而无法求解.
13.8点拨:由平行四边形的性质及面积公式和三角形的面积公式可得: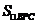 =
= ,∴
,∴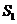 +
+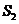 =
= .由三角形的中位线定理及相似三角形的性质等可得
.由三角形的中位线定理及相似三角形的性质等可得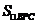 =4S=8,∴
=4S=8,∴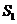 +
+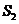 =8.
=8.
二、11. 1∶2 点拨:∵点D,点E分别是边AB,AC的中点,∴DE是△ABC的中位线,∴DE∥BC,且DE∶BC= 1∶2,故△ADE和△ABC的周长之比为1∶2.
12. 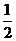
9.B 10.B
8.A点拨:∵AB∥CD,∴∠CDB=∠DBA,又∵∠C=∠BDA=90°,∴可判定△CDB∽△DBA,利用相似三角形的对应边成比例,即可判断各选项的正误.
7.B 点拨:先根据平行四边形的性质及相似三角形的判定定理得出△DEF∽△BAF,再根据 ∶
∶ =4∶25即可得出其相似比,由相似三角形的性质即可求出 DE∶EC的值.
=4∶25即可得出其相似比,由相似三角形的性质即可求出 DE∶EC的值.
6.B 点拨:根据相似三角形对应边的比等于相似比可得答案.
5.C点拨:∵∠BAD=∠C,∠ABD=∠CBA,∴△BAD∽△BCA,∴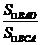 =
= =
=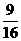 ,即
,即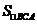 =
= ,∴
,∴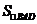 =
=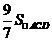 ,∴
,∴ =
=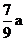 .本题考查的是相似三角形的判定与性质.根据两角对应相等判断两三角形相似,然后根据相似三角形面积的比等于相似比(即对应边的比)的平方列比例式,从而可知三角形的面积之间的关系.
.本题考查的是相似三角形的判定与性质.根据两角对应相等判断两三角形相似,然后根据相似三角形面积的比等于相似比(即对应边的比)的平方列比例式,从而可知三角形的面积之间的关系.
4. D 点拨:可利用特殊值法或比例的性质解题,也可用参数法解答,即先设出b=5k,得出a=13k,再把a,b的值代入即可求出答案.
一、1.B 2.B
3. B 点拨:方法一:由勾股定理得BC= ,AB=
,AB=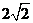 ,AC=
,AC=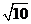 .选项A中三角形的三边长是2,
.选项A中三角形的三边长是2,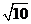 ,
,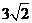 ;选项B中三角形的三边长是2,4,
;选项B中三角形的三边长是2,4,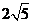 ;选项C中三角形的三边长是2,3,
;选项C中三角形的三边长是2,3,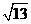 ;选项D中三角形的三边长是
;选项D中三角形的三边长是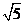 ,
,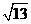 ,4.其中对应边的比相等的只有
,4.其中对应边的比相等的只有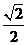 =
=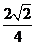 =
= ,∴与△ABC相似的三角形是选项B中的三角形.
,∴与△ABC相似的三角形是选项B中的三角形.
方法二:易知△ABC是两直角边长之比为1∶2的直角三角形,从而可快速找出正确选项B.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com