一、选择题

1.下列说法：①在同一个圆中，圆心角大的扇形面积大；②半径相等的两个圆叫做等圆；③圆的直径是圆的弦；④小于半圆的弧叫做优弧，其中正确的有（　　 ）

A.1个　　　 B.2个　　　 C.3个　　　 D.4个

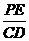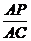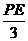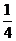24.解：（1）能.理由：当t=1时，AP=1 cm，BQ=1.25 cm.∴QD=BD-BQ=2-1.25=0.75 cm.∵PE∥BC，∴△APE∽△ACD,∴=，即=,∴PE=0.75 cm.∴PE=QD,∴四边形EQDP是平行四边形.

（2）AP=t cm，CP=（4-t） cm，BQ=1.25t cm，CQ=（5-1.25t） cm.∵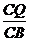==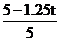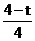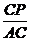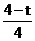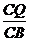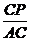，=，∴=，∴PQ∥AB.（3）当∠EQD=90°时，△EDQ∽△ADC,∴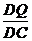=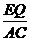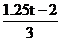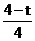，∴=，解得t=2.5.当∠DEQ=90°时，△DEQ∽△DCA,∴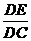=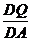.∵PE∥BC，∴△APE∽△ACD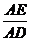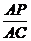，∴=，即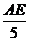=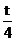，∴AE=1.25t cm，DE=AD-AE=（5-1.25t）cm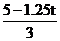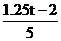，∴=，解得t=3.1.∴当t为2.5或3.1时，△EDQ为直角三角形.

23.（1）证明：∵∠ACD =∠BCE，∴∠ACE =∠DCB.

在△ACE和△DCB中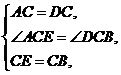，∴△ACE≌△DCB.

（2）解：△AMC∽△DMP.理由如下：由（1）知△ACE≌△DCB，∴∠CAE =∠CDB.又∵∠AMC =∠DMP，∴△AMC∽△DMP.

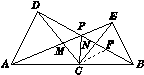
答图3

（3）证明：在DB上截取DF=AP，连结CF，如答图3.由（1）知△ACE≌△DCB，∴∠CAE =∠CDB.

又∵CA = CD，AP=DF，

∴△ACP≌△DCF，

∴∠APC=∠DFC，CP=CF,

∴∠BPC =∠DFC，

∴∠APC =∠BPC.

22.（1）证明：∵直径AB⊥CD,∴=,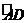

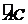∴∠ACH=∠F.又∵∠HAC=∠CAF，∴△ACH∽△AFC.（2）解：AH·AF=AE·AB.连结FB.∵AB是⊙O的直径，CD⊥AB,∴∠AFB=∠AEH=90°.又∵∠EAH=∠FAB，∴△AEH∽△AFB,∴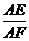=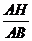,即AH·AF=AE·AB.（3）

点拨：本题利用了相似三角形的判定和性质，考查了同学们综合运用知识的能力.

21.解：由题图，观察者从左向右走到点E时，他的眼睛的位置点F与两棵树的顶端点A、C恰好在一条直线上.∵AB⊥l，CD⊥l，∴AB∥CD，∴△AFH∽△CFK，∴FH∶FK=AH∶CK，即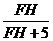==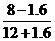，解得FH=8（m）.

∴当他与左边较低的树的距离小于8 m时，就不能看到右边较高的树的顶端点C.

20.解：如答图2所示，四边形A′B′C′D′即为所求.

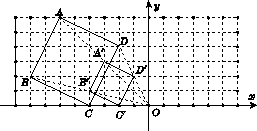
答图2

19.解：由已知得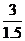=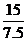，即3与1.5，15与7.5对应成比例.由△ABC∽△A′B′C′，可得它们的相似比为2.设△A′B′C′的第三边的长为x，由相似三角形的对应边成比例，得14∶x＝3∶1.5，所以x=7，即△A′B′C′的第三条边的长为7.

三、17.证明：因为AD=1，BD=2，AC=，所以AB=3.所以==，=，所以=.又因为∠A=∠A，所以△ACD∽△ABC.

18.证明：在△ABC中，AB=AC，BD=CD，∴AD⊥BC.又∵CE⊥AB，∴∠ADB=∠CEB=90°，又∵∠B=∠B，∴△ABD∽△CBE.

点拨：本题主要考查等腰三角形的性质及三角形相似的判定，要判定有一对角对应相等的两个三角形相似，只需再证得另一对角对应相等即可.

16.12 点拨：如答图1所示，延长BQ交射线EF于M，根据三角形的中位线平行于第三边可得EF∥BC，则△MEQ∽△BCQ,根据两直线平行，内错角相等可得∠M=∠CBM，再根据角平分线的定义可得∠PBM=∠CBM，从而得到∠M=∠PBM，根据等角对等边可得BP=PM，求出EP+BP=EM，再根据CQ= 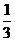CE求出EQ=2CQ，然后根据△MEQ和△BCQ相似，利用相似三角形的对应边成比例列式求解即可.

15.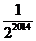 点拨：用从一般到特殊法解题，因为连结各边的中点所得到的三角形都与原三角形相似，所以周长比等于相似比.又因为第一个三角形的周长为1，所以第二个三角形的周长是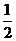，第三个三角形的周长是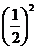，…，以此类推，第n个三角形的周长是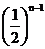，所以第2 015个三角形的周长为.

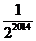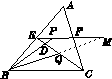
答图1