
18.请你依据下面图框中的寻宝游戏规则,探究“寻宝游戏”的奥秘:
(1)用树状图表示出所有可能的寻宝情况;
(2)求在寻宝游戏中胜出的概率.

图3
三、解答题
17.王强与李刚两位同学在学习“概率”时,做掷骰子(均匀正方体形状)试验,他们共掷了54次,出现向上点数的次数如下表:
|
向上 点数 |
1 |
2 |
3 |
4 |
5 |
6 |
|
出现 次数 |
6 |
9 |
5 |
8 |
16 |
10 |
王强说:“根据试验,一次试验中出现向上点数为5的概率最大.”
李刚说:“如果掷540次,那么出现向上点数为6的次数正好是100次.”
请判断王强和李刚说法的对错.
16.如图2,将转盘等分成六个扇形,并在上面依次写上数字1,2,3,4,5,6,指针的位置固定,自由转动转盘一次,当它停止时,指针落在偶数区域的概率是(指针落在两个扇形的交线时重转)______;请你用这个转盘设计一个游戏,当自由转动转盘一次,转盘停止时,指针所落区域的概率为13:____________________.
15.2013年1月11日,云南省昭通市镇雄县果珠乡高坡村赵家沟村民组发生山体滑坡,造成重大人员伤亡,需要空投救灾物资到指定的区域(⊙A),如图1所示,若空投救灾物资落在中心区域(⊙B)的概率为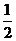 , 则⊙B与⊙A的半径之比为_______.
, 则⊙B与⊙A的半径之比为_______.

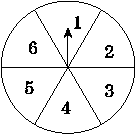
图1 图2
14.一个不透明的口袋里有10个黑球和若干个黄球,从口袋中随机摸出一球记下其颜色,再把它放回口袋中摇匀,重复上述过程,共试验200次,其中有120次摸到黄球,由此估计袋中的黄球有_______个.
13.在一个不透明的布袋中装有2个白球和n个黄球,它们除颜色不同外其余均相同.若从中随机摸出一个球,摸到黄球的概率是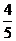 ,则n=_____.
,则n=_____.
12.从数字1,2,3中任取两个不同数字组成一个两位数,则这个两位数大于21的概率是________.
二、填空题
11.“明天下雨的概率为0.99”则“明天下雨”是________事件.
10.(2013,连云港)在一个不透明的布袋中,红球、黑球、白球共有若干个,除颜色外,形状、大小、质地等完全相同,小新从布袋中随机摸出一球,记下颜色……如此大量的摸球试验后,小新发现其中摸出红球的频率稳定于20%,摸出黑球的频率稳定于50%.对此试验,他总结出下列结论:①若进行大量的摸球试验,摸出白球的频率应稳定于30%;②若从布袋中随机摸出一球,该球是黑球的概率最大;③若再摸球100次,必有20次摸出的是红球.其中说法正确的是( )
A.①②③ B.①②
C.①③ D.②③
9.现有A,B两枚均匀的小立方体,小立方体的每个面上分别标有数字1,2,3,4,5,6.用小刚掷A立方体朝上的数字x,小明掷B立方体朝上的数字y来确定点P(x,y),那么他们各掷一次所确定的点P落在抛物线y=-x2+4x上的概率为( )
A.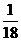 B.
B.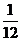 C.
C.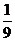 D.
D.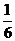
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com