12．桌上放着红桃、黑桃和梅花三种牌，共20张，下列判断正确的是(　)

①桌上至少有一种花色的牌少于6张；②桌上至少有一种花色的牌多于6张；③桌上任意两种牌的总数将不超过19张．

A．①②　 　　　　　　　　　　　　　　　　　　 B．①③

C．②③　 　　　　　　　　　　　　　　　　　　 D．①②③

答案　C

11．用反证法证明命题：“若a，b∈N，ab能被5整除，则a，b中至少有一个能被5整除”，那么假设的内容是(　)

A．a，b都能被5整除

B．a，b都不能被5整除

C．a，b有一个能被5整除

D．a，b有一个不能被5整除

答案　B

10．在平面直角坐标系中，直线x－y＝0与曲线y＝x²－2x所围成的面积为(　)

A．1　 　　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　　　 D．9

解析　如图所示

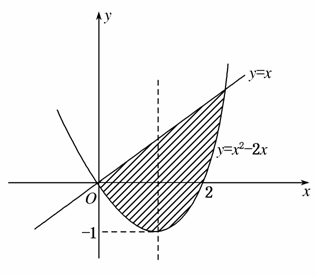
由得交点(0,0)，(3,3)．

∴阴影部分的面积为

S＝(x－x²＋2x)dx

＝(－x²＋3x)dx

＝(－x³＋x²)

＝－9＋＝.

答案　C

9．曲线y＝x³＋x²在点T(1，)处的切线与两坐标轴围成的三角形的面积为(　)

A.　 　　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　　 D.

解析　y′＝x²＋x，y′|_x＝1＝2，∴切线方程为

y－＝2(x－1)，与坐标轴的交点分别为(0，－)，(，0)，故切线与坐标轴围成的三角形的面积S＝××＝.

答案　D

8．设a>0，b>0，则以下不等式中不一定成立的是(　)

A.＋≥2　 　　　　　　　　　　　　　　　　 B．ln(ab＋1)≥0

C．a²＋b²＋2≥2a＋2b　 　　　　　　 D．a³＋b³≥2ab²

解析　易知A、B正确．

又a²＋b²＋2－(2a＋2b)

＝(a－1)²＋(b－1)²≥0，

∴C正确．

答案　D

7．对任意实数x，有f(－x)＝－f(x)，g(－x)＝g(x)，且x>0时，有f′(x)>0，g′(x)＞0，则x<0时，有(　)

A．f′(x)>0，g′(x)>0　 　　　　　　 B．f′(x)<0，g′(x)>0

C．f′(x)<0，g′(x)<0　 　　　　　　 D．f′(x)>0，g′(x)<0

解析　由f(－x)＝－f(x)及g(－x)＝g(x)知，f(x)为奇函数，g(x)为偶函数，由函数奇偶性的性质得f′(x)>0，g′(x)<0.

答案　D

6．用数学归纳法证明不等式1＋＋＋…＋<n(n∈N^*且n>1)时，第一步应验证不等式(　)

A．1＋<2　 　　　　　　　　　　　　　　　　 B．1＋＋<2

C．1＋＋<3　 　　　　　　　　　　　　　 D．1＋＋＋<3

答案　B

5．已知函数f(x)＝－x³＋ax²－x－1在(－∞，＋∞)上是单调函数，则实数a的取值范围是(　)

A．(－∞，－]∪[，＋∞)

B．[－，]

C．(－∞，－)∪(，＋∞)

D．(－，)

解析　f′(x)＝－3x²＋2ax－1，

若f(x)在(－∞，＋∞)上为单调函数只有f′(x)≤0，

∴Δ＝(2a)²－4(－3)(－1)≤0，

解得－≤a≤.

答案　B

4．函数y＝f(x)在区间[a，b]上的最大值是M，最小值是m，若m＝M，则f′(x)(　)

A．等于0　 　　　　　　　　　　　　　　　　　 B．大于0

C．小于0　 　　　　　　　　　　　　　　　　　 D．以上都有可能

答案　A

3．已知数列2,5,11,20，x,47，…合情推出x的值为(　)

A．29　 　　　　　　　　　　　　　　　　　　　　 B．31

C．32　 　　　　　　　　　　　　　　　　　　　　 D．33

解析　观察前几项知，5＝2＋3，

11＝5＋2×3,20＝11＋3×3，

x＝20＋4×3＝32,47＝32＋5×3.

答案　C