
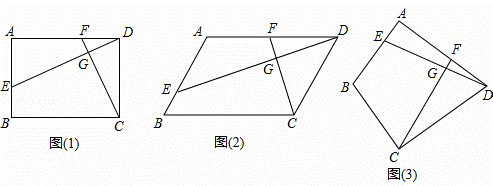
1.(2013•武汉)已知四边形ABCD中,E,F分别是AB,AD边上的点,DE与CF交于点G.
(1)如图①,若四边形ABCD是矩形,且DE⊥CF.求证: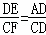 ;
;
(2)如图②,若四边形ABCD是平行四边形.试探究:当∠B与∠EGC满足什么关系时,使得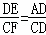 成立?并证明你的结论;
成立?并证明你的结论;
(3)如图③,若BA=BC=6,DA=DC=8,∠BAD=90°,DE⊥CF.请直接写出 的值.
的值.
27、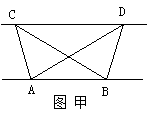 (本题满分11分)
(本题满分11分)
(1)探究新知:如图甲,已知△ABC与△ABD
的面 积相等,则AB与CD的位置关系是
.
积相等,则AB与CD的位置关系是
.
(2)结论应用:
① 如图乙,点M,N在反比例函数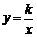 (k>0)的图象上,
(k>0)的图象上,
过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.试证明:MN∥EF.
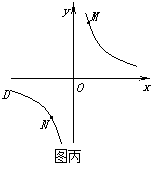
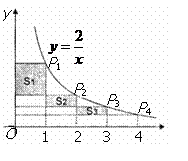
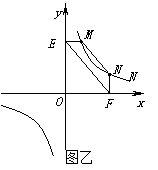 ② 若①中的其他条件不变,只改变点M,N的位置如图丙所示,请判断 MN与EF是否平行.
② 若①中的其他条件不变,只改变点M,N的位置如图丙所示,请判断 MN与EF是否平行.
26、(10分)已知反比例函数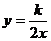 和一次函数
和一次函数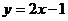 ,且一次函数的图像经过
,且一次函数的图像经过
(a,b)和(a+1,b+k)两点.
(1)求反比例函 数的解析式;
数的解析式;
(2)若直线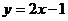 上有一点A(1,c),则点A在
上有一点A(1,c),则点A在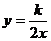 上吗?说明理由.
上吗?说明理由.
(3)利用(2)的结果,说明在x轴上是否存在点P,使△AOP为等腰三角形?若存在,直
接写出P点坐标.
25.(9分)已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.
(1)求证:△ADE≌△CBF;
 (2)若四边形BEDF是菱形,则四边形AGBD是什么特殊的四边形?
(2)若四边形BEDF是菱形,则四边形AGBD是什么特殊的四边形?
并证明你的结论。
24、(8分)市政府的一项实事工程是由政府投人1 000万元资金,对城区4万户家庭的老式水龙头和13升抽水马桶进行免费改造.某社区为配合政府完成该项工作,对社区内1200户家庭中的120户进行了随机抽样调查,并汇总成下表:
|
改造 情况 |
均不 改造 |
改造水龙头 |
改造马桶 |
||||
|
1个 |
2个 |
3个 |
4个 |
1个 |
2个 |
||
|
户数 |
20 |
31 |
28 |
21 |
12 |
69 |
2 |
(1)试估计该社区需要对水龙头、马桶进行改造的家庭共有_____户;
(2)改造后,一只水龙头一年大约可节省5吨水,一只马桶一年大约可节省15吨水.试估计该社区一年共可节约多少吨自来水?
(3)在抽样的120户家庭中,既要改造水龙头又要改造马桶的家庭共有多少户?
23、(7分)如图,在平面直角坐标系内,已知OA=OB=2,∠AOB=30°.
(1) 点A的坐标为( ,
);
点A的坐标为( ,
);
(2)将△AOB绕点O顺时针旋转a度(0<a<90).
①当a=30时,点B恰好落在反比例函数y=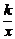 (x>0)的图象上,求k的值;
(x>0)的图象上,求k的值;
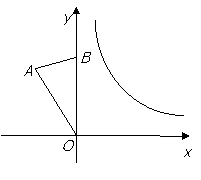 ②在旋转过程中,点A、B能否同时落在上述反比例函数的图象上,若能,求出a的
②在旋转过程中,点A、B能否同时落在上述反比例函数的图象上,若能,求出a的
 值;若不能,请说明理由.
值;若不能,请说明理由.
22、(6分)某商场出售一批进价为2元的贺卡,在市场营销中发现商品的日销售单价x元与日销售量y个之间有如下关系:
|
x(元) |
3 |
4 |
5 |
6 |
|
y(个) |
20 |
15 |
12 |
10 |
(1)根据表中数据,在直角坐标系描出实数对(x,y)的对应点
(2)猜测并确定y与x之 间的函数关系式,并画出图象;
间的函数关系式,并画出图象;
(3)设经营此贺卡的销售利润为w元,试求出w与x之间的函数关系式,若物价居规定此贺卡的售价最高不能超过10元/个,请你求出当日销售单价x定为多少元时,才能获得最大日销售利润?
2.B布袋中有三个完全相同的小球,分别标有数字-2,-3和-4.小明从A布袋中随机
取出一个小球,记录其标有的数字为x,再从B布袋中随机取出一个小球,记录其标有的
数字为y,这样就确定点Q的一个坐标为(x,y).
(1)用列表或画树状图的方法写出点Q的所有可能坐标;
(2)求点Q落在直线y=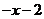 上的概率.
上的概率.
21、(6分)有A、B两个黑布袋,A布袋中有两个完全相同的小球,分别标有数字1和
20、(5分)已 知
知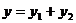 ,
,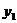 与
与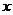 成正比例,
成正比例,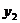 与
与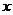 成反比例,且当
成反比例,且当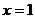 时,
时,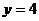 ,
,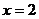 时,
时,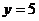 .
.
求:(1) 与
与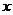 之间的函数关系式. (2)当
之间的函数关系式. (2)当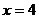
 时,求
时,求 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com